Lec2.3 Softmax Regression(2)

The softmax regression optimization problem

好的，现在让我们谈一谈Softmax回归的最后一个因素,即优化问题。

这可能是需要花费最多时间讨论的部分，因为我们需要稍微讲解一下如何优化这些参数，即何找到好的参数$θ$值？

机器学习算法的第三个因素实际上正在解决如下的优化问题

$$\min_{\theta} \frac{1}{m}\sum_{i=1}^{m} loss(h_{\theta}(x^{(i)} ), y^{(i)} )$$

• 这里的$minimize$符号表示优化问题，意味着我们正在搜索$\theta$的所有可能值，或至少试图搜索所有可能值，以使得$\frac{1}{m}\sum_{i=1}^{m} loss(h_{\theta}(x^{(i)} ), y^{(i)} )$最小化。

换而言之，每个机器学习算法都以一种方式寻找一组参数，这些参数最小化训练集上某些预测和真实标签之间的损失函数的总和(或者平均值)。实际上，这个公式已经确实包括机器学习算法的所有方面，它包括假设函数($h_{\theta}(x^{(i)})$),损失函数($loss()$)和优化问题($\min_{\theta}$)。因此，这个问题，可能会有一些轻微的变化（比如添加正则化），但在深度学习中我们通常不会那么做。每个算法，每个机器学习算法都以某种方式解决类似于这样的问题。至少每个监督算法，也可能每个无监督算法。

现在我们可以具体看一下像Softmax回归这样的东西看起来是什么样子：

$$\min_{\theta} \frac{1}{m}\sum_{i=1}^{m} loss_{ce}({\theta}^{T }x^{(i)} , y^{(i)} )$$

通过寻找更好的$\theta$使损失函数最小化，这部分是相同的，然后我们要做的就softmax回归的具体信息。

• 使用交叉熵损失函数

• 我们的假设函数是线性的，是${\theta}^{T }x^{(i)}$

这就是我们要为Softmax回归解决的优化问题。当然，问题是，我们实际上如何找到这个参数矩阵的$\theta$值?(该$\theta$为输入和输出之间提供良好映射)。

---

Optimization : gradient descent

我们要使用一种叫做梯度下降的技术来实现这个目标。

但是为了讲解梯度下降，我首先想谈谈梯度。

假设我们有一个矩阵输入、标量输出的函数。也就是说，这是一个从$n\times k$向量映射到实数的函数,我们将用$f$表示这个映射。

按深度学习的例子来说,$\theta$ 就表示假设函数，$\theta\in \mathbb{R}^{n\times k}$ ,$f(\theta)$ 就表示优化问题里的损失函数

那么，在使$f(\theta)$最小化方面，我们应该怎么做呢？一种非常好的方法是使用梯度。梯度是一个由这个函数各个偏导数组成的矩阵。特别地，如果函数本身或函数的输入是$n×k$维度的，则在这里非常重要的是梯度，我们将其写为这个小倒三角形。关于$f(\theta)$的$\theta$梯度（我们通常这样写）也将是一个$n×k$矩阵。它将仅是此函数的所有偏导数的矩阵。因此，第一个元素将只是相对于$\theta_{11}$ 的$f(\theta)$的偏导数,到最后一行的最后一个元素将是相对于$\theta_{nk}$的$f(\theta)$的偏导数。这些偏导数的符号意味着，正在将$\theta$的每个其他元素视为一个常量，求导的时候$f(\theta)$只是$\theta_{11}$的函数。

这就是梯度的定义。

现在我真正应该提到的一件事是，这里的符号确实很糟糕。但这是人们使用的东西，所以我们必须在某种程度上习惯它。因为如果函数有许多参数，你需要某种指定要相对于哪个参数进求导的方式。这就是这个下标在这里的含义，对吧？它只是说我们正在针对哪个参数进行求导。很抱歉，符号很差。我们在机器学习中使用了很多不良符号。但我有意包括不良符号而不是使用更好的符号。有些人会在这里使用索引，他们会使用1、0或类似的东西。那是客观更好的符号，但它并不常见。因此，我将使用通用但糟糕的符号，您必须遗憾地习惯它。

现在，这个梯度的好处是，它指向指向$f(\theta)$最大增长的方向,这是一个非常强有力的概念。类似于在一维微积分中，导数等于该函数的斜率，那么在高维度中这就是梯度。如果$\theta$是一个向量值，那么梯度将是一个向量。它指向f的最大增长方向，至少在局部范围内。通过一点微积分，你至少在局部范围内已经拥有了在参数空间中增加函数最多的方向，并且我们将会看到，通常存在计算梯度的有效方法。这是自动微分的内容，但我们可以非常高效地计算它。通过这样做，我们可以轻松地找出如何更改或优化我们的参数$\theta$。

---

Optimization : gradient descent

那么我们该如何做到这一点呢？好的，这立即引导我们到我会提出的几乎所有机器学习算法的核心算法。

如果梯度指向最大增加的方向，那么如果我们想要最小化我们的函数:

我们可以将$\theta$设置为$\theta$减去其梯度的某个倍数$\alpha$。

$$\theta:=\theta-\alpha\nabla_{\theta} f(\theta)$$

这里$\alpha$被称为步长或学习率,它只是一些小的正量。所以我们减去梯度的一些小的正倍数。矩阵的大小也是正确的，因为在我们的情况下，$\theta$是$n\times k$，$\theta$的梯度也是$n \times k$，乘以一个标量只是缩放。因此，这是我们可以进行的有效更新，

关键思想是，因为梯度指向最大增加的方向，如果我们想要最小化函数，那么减去梯度的一小部分会导致$f(\theta)$变小，现在，在我进入细节之前，我必须花一分钟来感受这种方法的力量。因此，毫不夸张地说，梯度下降的这个基本思想支配了所有深度学习。

也许不是，可能还有一些人偶尔使用的无梯度方法，但是99％的所有深度学习以及因为深度学习在这里如此普遍，你看到的所有AI的90％都是基于这一行数学构建的。所以，上次演讲中那些狗，狗教授的图像，大型语言模型AlphaFold，它们都是基本上使用了这个算法。出于某种原因，这个算法仍然没有被广泛地教授在他们的第一个本科课程中，我认为这很疯狂。这是一个根本性的算法，很难夸大梯度下降对机器学习领域乃至整个世界的影响，从根本上说，现在这个算法是所有深度学习的基础。当然，当我说梯度下降时，我指的是梯度下降及其变体，包括任何基于梯度的优化技术。

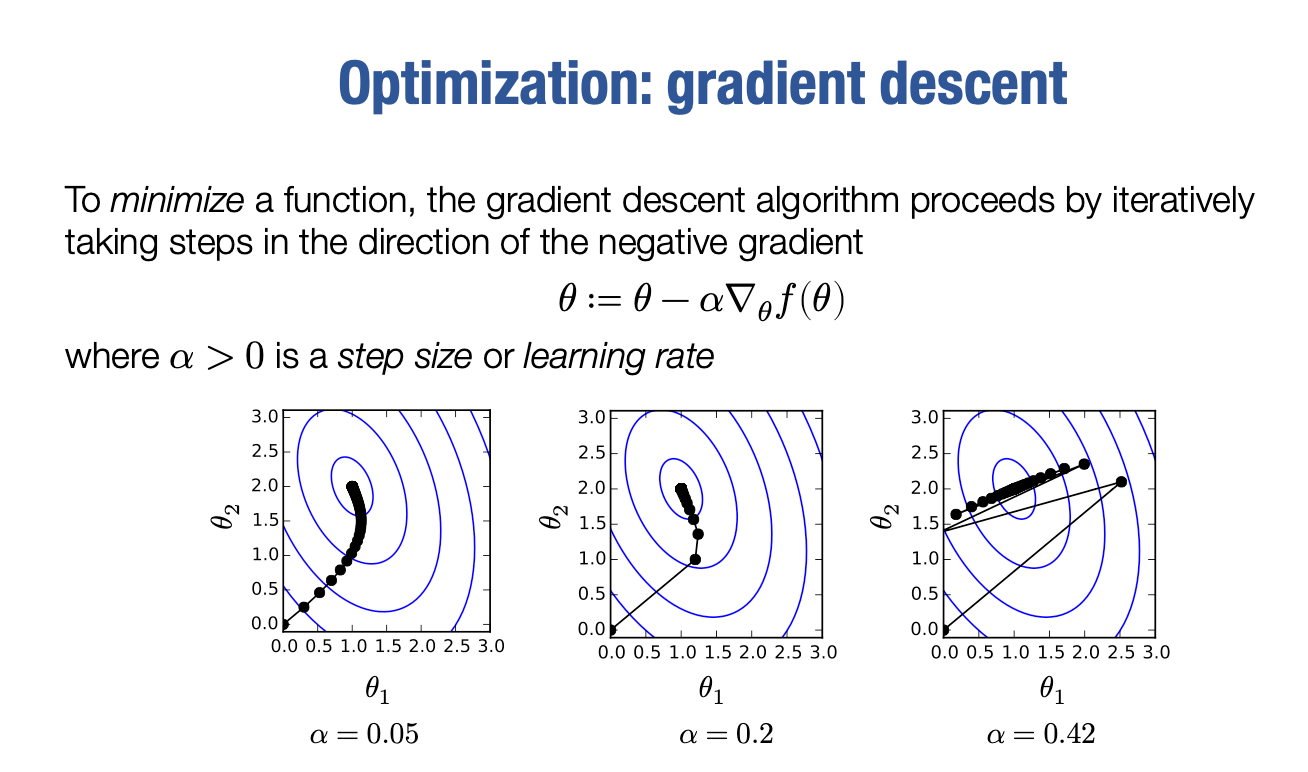
现在，你在这里可能会有一个大问题，即我们应该为此$\alpha$选择什么值,我们该走多大的步长？事实证明，这里的$\alpha$的选择极大地影响了优化的过程。因此，如果采取小的$\alpha$，我这里展示了另一个简单的函数。

• 如果采取小的梯度步长，会取得小而缓慢的进展,会逐渐朝最佳状态迈出小而稳定的步伐。

• 如果采取更大的步长,将会取得非常好的、快速、迅速的进展，朝最佳状态迈出更快的进展。

• 实际上，如果我们采取更大的步长，我们可以采取如此大的步长，以至于我们每次都会超过，并且使我们的函数增加，然后发散到无限远，不会完全遵循该路径，它会以不同的方式弹跳，我很难画它们的路径，但基本上你会开始发现它们发散，不收敛到任何东西。

因此，在选择如何优化此函数时，步长的选择非常重要。事实上，作为从现在开始的几节课的快速预览，如果你听说过像Adam或带有动量的梯度下降等优化方法，那些实质上尝试加速这个过程的方法，所以无需太担心步幅大小。

---

Stochastic gradient descent

好的，现在最终我要说的是，即使我们之前提到的最后一个算法，也不完全是深度学习中实际使用的东西。因为如果我们看一下我们的损失函数，我们试图优化的是什么？再次强调，我们试图最小化对于$\theta$的平均损失，这适用于通用机器学习，而不仅仅是softmax回归。

$$\theta:=\theta-\frac{\alpha}{m}\sum_{i=1}^{m} \nabla_{\theta} loss(h_{\theta}(x^{(i)} ), y^{(i)} )$$

整个式子的梯度要求从1到m的对于$\theta$的梯度之和。问题在于，如果数据集越来越大，那么m越来越大，我们将需要求越来多的梯度，这真的很浪费时间。想象在拥有无限数据的极限情况下，我们实际上将没有任何进展，因为我们只会永远计算我们的梯度，这似乎不是正确的方法。还存在其他问题,特别是在深度学习中，如果我们尝试计算所有数据的梯度，将会耗尽内存,无法将所有数据放入内存中，更别说需要在内存中计算梯度的术语了。

因此，深度学习真正做的事情，不是运行经典的梯度下降，而是运行称为随机梯度下降(SGD) 的变体。现在，理论上可以将SGD制定为随机最小化过程，其中有一些期望为真梯度的随机变量，但具有某些方差，这是SGD的数学解释。

在实践中，SGD的意思是，只需将数据集分成所谓的“ minibatches”。这些基本上是数据的子集，大小为$B$。因此，在随机梯度下降中，我们首先对数据进行小批量采样,我们实际上通常将整个数据集分成若干个部分，使每个部分都有$B$个样本。然后，只需循环遍历所有这些大小为$B$的子集。所以大致步骤是这样的

• 第一步，我们获取大小为$B$的子集，其中既包括输入矩阵的$B$个样本，也包括相应的输出。

• 第二步，现在，依然通过采取梯度步骤来更新参数，

$$\theta:=\theta-\frac{\alpha}{B}\sum_{i=1}^{B} \nabla_{\theta} loss(h_{\theta}(x^{(i)} ), y^{(i)} )$$

就好像我们的损失只是这$B$个样本一样。因此，要思考的方式是，我们在这里采取的每一步都只是对真正梯度的粗略近似，但是这会加速计算过程，实际上，在深度学习中甚至有时会有优势，因为我们通常会有一些噪音，实际上在某些情况下会有所帮助。

因此，虽然它是我们认为理想化优化过程的近似，但是我们可以更快，更容易地进行优化。因此，与其总和，强调这个等式上的内容，我们只需对所有$B$求和，这样计算速度更快，因为只有$B$个而不是数百万个示例。

现在我可以更正式地说，事实上，这就是推动近年来你在深度学习中看到的所有进展的算法。这是几乎所有深度学习算法的训练方式，稍微变异一下即可。我们稍后将讨论如何实际执行这些更常见的方法，如动量或Adam等。

好的，这就是优化过程，

这是softmax回归算法的第三个组成部分。

---

The gradient of the softmax objective

但是为了最终确定它，我们还有最后一步，那就是我们如何实际计算与我们的参数$\theta$相关的损失之和的梯度？

换句话说，我们如何计算梯度，如果我们可以计算其中一个术语的梯度，我们可以将它们全部加在一起，以获得整个目标的梯度。那么我们该怎么做呢？嗯，事实证明这并不难，但也不容易。

实际上，当我学习机器学习时，这就是我们做的事情,你设计一个新的目标并亲手推导出所有梯度。我们现在生活在更好的时代。事实上，大多数情况下，当你开发模型时，你将不必这样做。实际上，自动微分的整个重点，即我们将在几堂课程中介绍的内容 。

如果我诚实地说，正确地执行其实非常繁琐，但让我们先从一个错误的问题开始。让我们从把$h$，不作为假设函数，而只是一个向量开始。这将是我们推导的一个步骤。让我们看看能否仅将$h$作为向量处理，计算交叉熵损失函数的梯度。因此，我基本上想计算这个东西，但请记住梯度的元素只等于损失函数的偏导数。因此，我首先要计算我的梯度。我将首先计算关于$h_i$的偏导数

我要再次写下我们的损失函数：

$$l_{ce}(h,y )=-h_y + \log\left(\sum_{j=1}^k \exp(h_j)\right)$$

现在求偏导

根据链式法则，我们需要分别求出$l_{ce}$关于$h_i$的偏导数：

$$\frac{\partial l_{ce}}{\partial h_i} = -\frac{\partial h_y}{\partial h_i} + \frac{1}{\sum_{j=1}^k \exp(h_j)}\frac{\partial}{\partial h_i}\left(\sum_{j=1}^k \exp(h_j)\right)$$

首先考虑第一项：

$$-\frac{\partial h_y}{\partial h_i}=-\frac{\partial}{\partial h_i}(h_i)= -1$$

然后考虑第二项，根据指数函数的求导公式：

$$\frac{\partial}{\partial h_i}\left(\exp(h_j)\right)=\begin{cases} \exp(h_i) & i=j \\ 0 & i\neq j \end{cases}$$

因此，

$$\frac{\partial}{\partial h_i}\left(\sum_{j=1}^k \exp(h_j)\right)=\sum_{j=1}^k \frac{\partial}{\partial h_i}\left(\exp(h_j)\right)=\exp(h_i)$$

将上述结果代入原式中，得到：

$$\frac{\partial l_{ce}}{\partial h_i} = -\delta_{iy} + \frac{\exp(h_i)}{\sum_{j=1}^k \exp(h_j)}$$

• 其中，$\delta_{iy}$是Kronecker delta符号，当$i=y$时为1，否则为0。

我们现在可以更好地用向量形式写出这整个导数:

$$abla_{h} l_{ce}(h,y)=\bold z- \bold e_y$$

• $\bold z=softmax(\bold h)$

• 向量$\bold e_y$在第y个位置为1,其他位置为0的单位向量

我们还记得之前说的softmax

$$z_i=\text{softmax}(x)_i = \frac{\exp(x_i)}{\sum_{j=1}^k \exp(x_j)}$$

因此，总结一下最终结果，这个项是将交叉熵损失相对于其输入视为向量的最终梯度。那么我们已经完成了吗？非常接近了，但在某种程度上还有些遥远

---