Lec3.1 From linear to nonlinear hypothesis class

这节课将延续上次我们手动推导softmax回归算法的线索。这一次，我们将以基本的全连接网络为例，采用与上次类似的方式进行推导。

这将是最后一节课采用我所谓的老式方法手动推导所有这些导数的方式。从下一节课开始，我们将采用更为通用的技术——自动微分。

然而，在本课中，我们将采用稍微繁琐一些的方式。如果你之前已经学过神经网络或实现过反向传播，那么很有可能你实现过类似的方法。虽然符号可能略有不同，但基本思路是相似的。

所以我们将通过这个例子来讲解，但是正如我所说的，这里的意图在于突出这些方法的复杂性，并激励我们寻求更通用的泛型形式。

The trouble with linear hypothesis classes

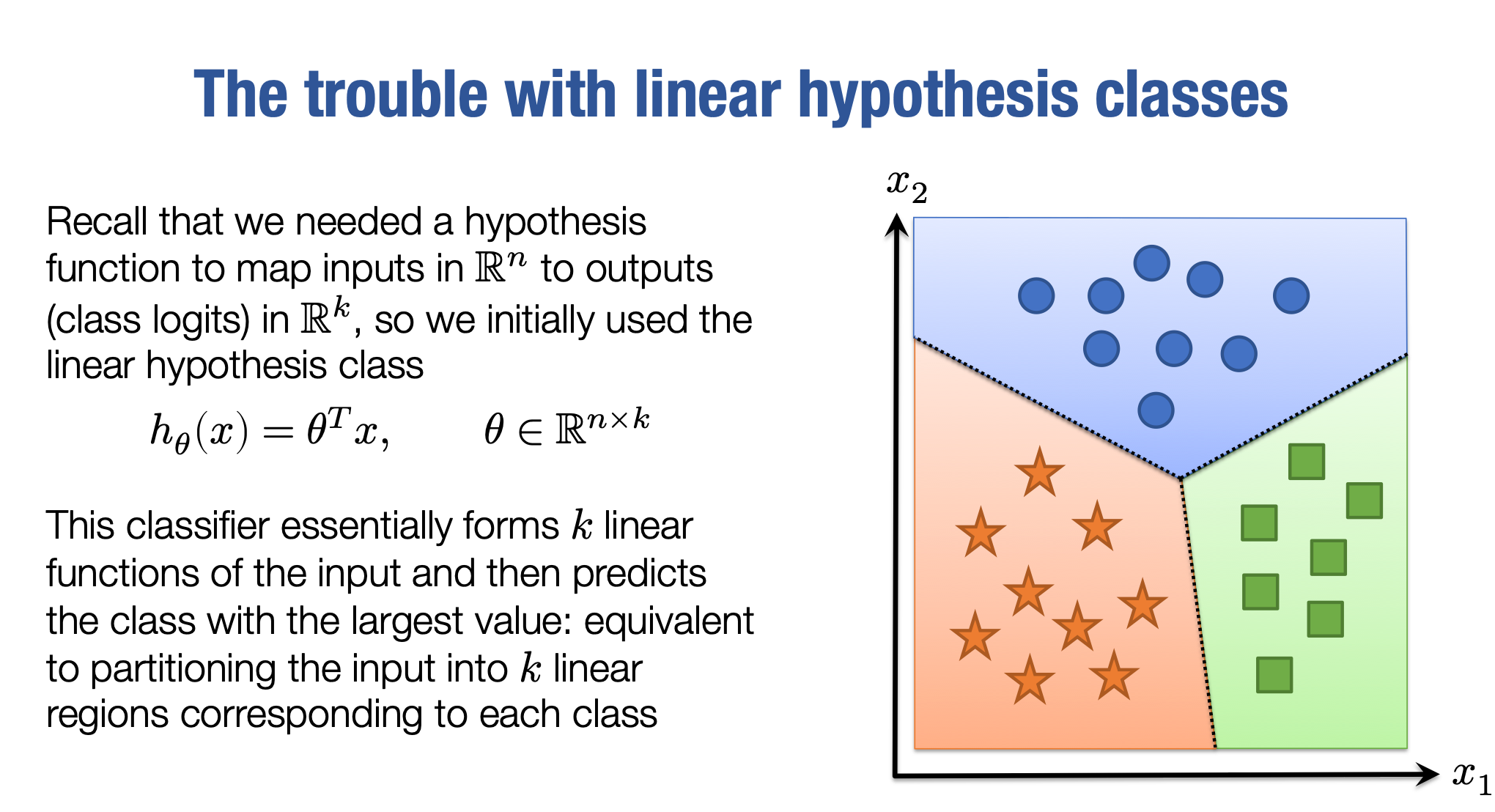
为了转向非线性假设类，我们要回顾上次讲过的基本线性假设类。还记得上次课我们说过，我们的假设类是基于x做的预测， 这是一个线性函数。即

$$h_{\theta}(x)=\theta^Tx$$

这里的$\theta$是一个$n \times k$的矩阵。因此，我们从n维输入映射到k维输出，这些输出就是我们所说的不同类别的logits，也就是K个不同类别的logits。现在，我们所描述的这个函数实际上是在对输入形成k个不同的线性函数，然后将预测的类别设置为其中具有最高值的类别，也就是这k个不同函数中具有最高值的那个函数。

$$h(x)=\begin{bmatrix} h_1(x)\\ h_2(x)\\ .\\ h_i(x)\\ .\\ h_k(x) \end{bmatrix}$$

你应该对这个函数有一个画面，在这个画面中，我们将空间分成了3个不同的线性区域，每个线性区域都代表一个类别。

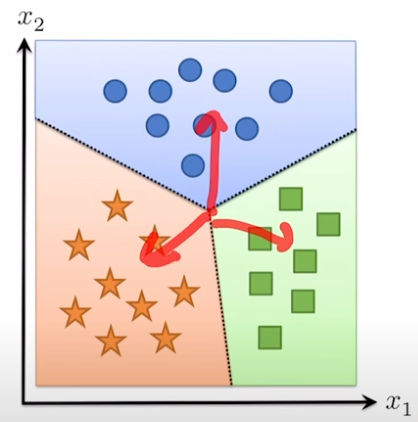
然后我们用这些假设类将空间分为如图的三个方向，现在这个三个方向的预测大小是$h_i(x)$。哪个方向预测的值最大，哪个方向就是我们预测的类别。因此，对于两个类别，这只是一个分隔正例和负例的线条。但是对于更多的类别，这仍然只是线性方向，我们根据哪个方向与我们的类别最接近来预测。

当然，问题在于这是一个非常有限的假设类，你可以想象出许多不适合这种模式的数据。

---

What about nonlinear classification boundaries

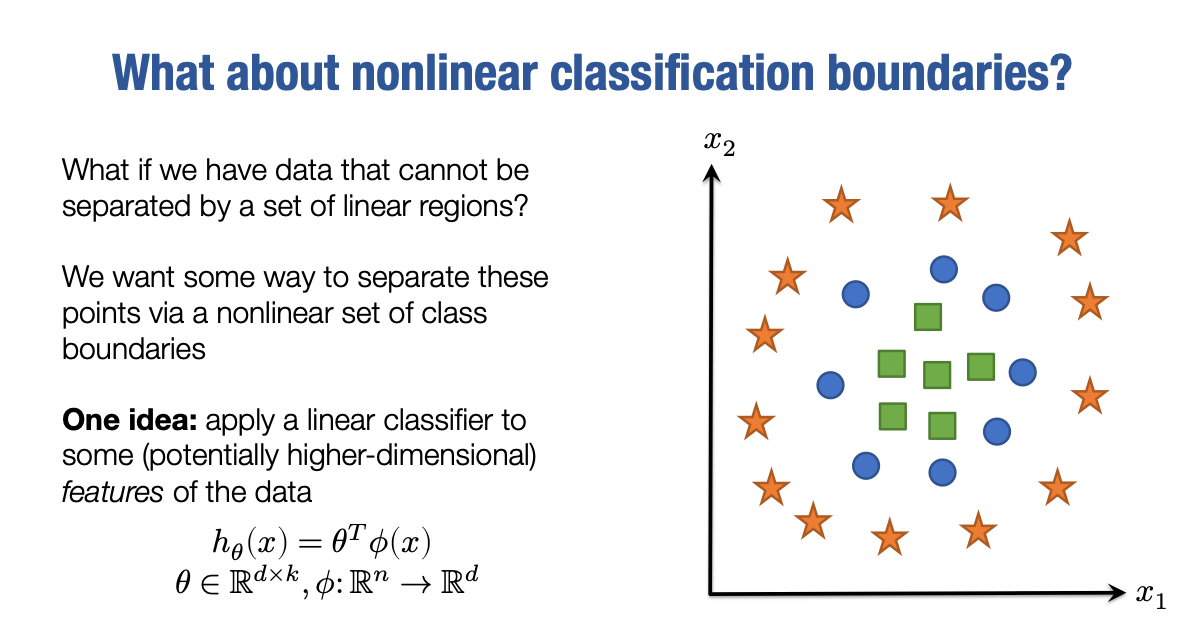
考虑我们之前的例子，数据被聚集到三个簇中。

现在考虑一个不同形式的数据集，绿色的样本位于这里，蓝色的样本位于这个带状区域内，橙色的样本则位于包围圆形的带状区域内。

很显然，没有线性分类器能够正确分类这三个集合的样本。然而，我们仍然希望有一种方法来分离这些区域或点。在高维空间中，我们相信我们要分离的实际类别将通过非线性关系进行分离。因此，我们需要的是超越线性假设类的分离数据的方法。这种方法的最初和自然的扩展是，我们的假设函数不再只是输入$x$的线性函数，而是输入函数$\phi(x)$的线性函数。

$\phi$是一个从$R^n$到$R^d$的映射函数，它是一个将我们的输入映射到一些更高维度或更低维度的表示空间（(即d维的特征）的函数。我们的最终假设类将只是这些特征的线性函数。手动从原始数据中提取一些特征，并将其馈入线性机器学习分类器中，是一种非常强大的范例。当你知道如何从数据中提取有价值的特征时，它仍然是实践中进行许多机器学习的有用方法。我们将专注于使用神经网络提取这些特征，但这是一个非常不同的概念，与手动提取特征的方式有所不同。然而，手动特征工程在许多机器学习中仍然扮演着非常重要的角色。但让我们深入思考一下我们可以选择什么样的特征映射，因为虽然手动提取特征在某些情况下可能是有用的，但我们需要思考更通用的特征形式。我们希望形成一组通用的特征，以便可以应用于任何问题。

---

How do we create features?

正如我所说的，我们可以通过手动设计创建这个特征函数$\phi$，对吧？从某种意义上说，这是做机器学习的老方法,这是人们长期以来采用的方法。

然而，我们也希望能够从数据中学习这些特征, 这实际上是推动神经网络整个概念的一种方式。

神经网络是一种从输入数据中提取良好特征的方式，但是它以一种自动化的方式进行，我们不必自己手动调整它们。我将其称为机器学习的旧与新方式。这有点玩笑话。实际上，这两种技术都非常强大，但本课程大部分将专注于思考是否可以从数据中学习特征提取器，也就是一种直接从数据中找到好的特征的方式。

线性函数对于预测是如此强大,我们能够使用仅使用线性分类器，在MNIST数字分类问题上获得8%的误差。因此，作为对此的第一次尝试，从$R^n$到$R^d$的映射函数也许我们可以再试一种线性函数?

所以我们试试这个函数

$$\phi(x)=W^Tx$$

• 其中$W$是一个$n \times d$的矩阵

然而，这实际上并不可行，因为如果你使用这种特征定义，并将其与线性分类器一起使用，那么会发生非常不幸的事情，即我们的新假设类是

$$h_{\theta}(x)=\theta^T\phi(x)=\theta^T W^Tx=\tilde \theta x$$

也就是说，我们在这里实际上只是应用了另一个线性分类器, 因此，这并不起作用。然而，非常相似的一些方法实际上是可行的。

---

Nonlinear features

我们可以定义我们的特征和特征映射基本和上面一样，但随后又应用于这个新特征向量的一些非线性函数$\sigma$。

在这里， $W$类似于之前的例子中的$n \times k$的矩阵，而$\sigma$是我们应用的任何函数，通常是对特征向量进行逐元素操作。但实际上，它不一定是逐元素的，它可以是任何形式的操作。通过这样的方式，我们获得了一个更强大的特征向量。

我们可以在这里做很多简单的事情，这些事情可以产生很强大的描述输入的特征。例如，如果我们让W是一个固定的矩阵，它是从高斯分布中随机采样的，那么我们就可以将它们缩放到正确的输出空间。这种方法称为随机傅里叶特征。在许多使用随机傅里叶特征的问题中，这种方法非常有效。

但我们并不总想限制自己的选择，这仍然是一种事先选择$\phi$的方法。我们指定一些映射，然后我们学习算法的所有内容就是我们学习算法的唯一参数$\theta$。因为在这里W被认为是固定的，所以它不是我们学习算法的参数。

但这引出了一个自然的问题：如果我们有这样的一个设置，也许我们也想优化W。也许我们可以通过某种方式训练或优化W来降低我们的损失，以此比仅将其视为一个固定矩阵或者$\phi$视为一个固定特征提取器做得更好。

这正是神经网络要做的事情。在这种解释中，神经网络可以被视为一种提取数据特征的方式，我们同时训练最终的线性分类器（即$\theta$），以及特征提取器（即$W$或更复杂的参数集合）。

如果我们将这个假设视为一个网络或假设类，其中$\theta$和$W$都是网络的参数，那么这个假设就是一个两层神经网络的最简单的情况。

​