Lec3.3 backpropagation

Neural networks in machine learning

为了先解释清楚，上次我们讨论到的“神经网络”，实际上只是机器学习算法的三个要素之一。这三个要素分别是假设类、损失函数和优化过程。你还记得吗？事实证明，与之前使用 softmax 回归时的情况一样，我们现在仍然会使用相同的两个要素。也就是说，我们仍然会使用交叉熵损失函数和随机梯度下降优化过程。这两个要素与之前完全相同。换言之，我们的优化问题实际上并没有改变，仍然是在参数上最小化假设与真实输出之间交叉熵损失的平均值。

唯一不同的是，我们的假设类现在不再只是线性函数，而是一个神经网络，可以是简单的两层神经网络或多层 L 层网络。当然，接下来我们很快会讨论更复杂和结构化的假设类。

那么这意味着，实现神经网络和softmax回归算法相比，实际上唯一的区别就在于我们需要一种方式来计算这些梯度，也就是关于$\theta$的梯度。当我说关于theta的梯度时，我实际上的意思当然是关于两组$W1$和$W2$参数的梯度,这就是唯一的区别。那么，我们现在就来深入研究一下，实际上这些梯度是什么,在这样做的过程中，我们将得出反向传播算法的实际规则。

The gradient(s) of a two-layer network

好的。当我说关于$\theta$的梯度时，我实际上指的是关于$W_1$的梯度，我们需要那个东西。我们需要关于我们关心的损失的梯度。在这里，我只是用我们的假设函数进行了替换。所以让我们来谈谈实际上，那个两层网络我之前提到的，我们的假设类实际上就是这个

我们想要的是这个假设类关于$W_1$和$W_2$的梯度，也就是我们所说的关于$\theta$的梯度，即这两个参数的梯度。好的。现在我们没有其他可做的事情，只能去实际做它。我们将使用上一节讲过的完全相同的技术。

我们要做的技巧是，我们将像所有这里的值都是标量值一样进行偏导数运算。然后我们将观察结果数量的大小，并确定我们的实际梯度必须是什么，以使这些大小能够起作用。

在这种情况下，我们采用了一种欺骗性的方式来计算所有这些梯度。在这种情况下，实际上检查我们的梯度变得更加重要，因为现在我们很容易犯很多错误，但这些实际上将是正确的梯度。这是我最后一次给你们展示这些内容了

在本讲之后，你们将能够安全地忽略很多这些内容，因为你们可以通过自动微分来很好地完成这些计算。好的，那么我们首先来计算相对于$W_2$的损失的梯度。这里的$W_2$是我们简单的两层网络中的第二层权重。

其中S是基本上等于我们分类器的最终预测应用softmax运算符得到的结果。

那么我们接下来的问题当然是，我们如何从这个公式中计算梯度呢？

我们知道这里的梯度，即关于$W_2$的梯度，以及因此关于$W_2$的梯度，将是一个$d\times k$的矩阵，为了使这些尺寸相符，我们要做的仍然是上次所做的完全相同的操作。

我们的梯度的最终形式就是

其中$I_y$则是整个数据集上标签的one-hot编码。

$I_y$是一个$m \times k$的矩阵，其中m是数据集中的样本数，k是类别的数量。每一行对应一个样本，每一列表示一个类别，而对应的位置上的元素值表示该样本是否属于该类别，是则为1，否则为0。

好的，这是比较简单的部分

The gradient(s) of a two-layer network

现在我们要深呼吸一下，接下来进行下一步。我们必须更新$W_1$和$W_2$两个参数，才能通过梯度下降实际进行更新。那么，关于 $W_1$，我们的交叉熵损失函数的导数是什么呢？

我们想要计算这个值，需要应用链式法则多次,我将写出具体的表达式:

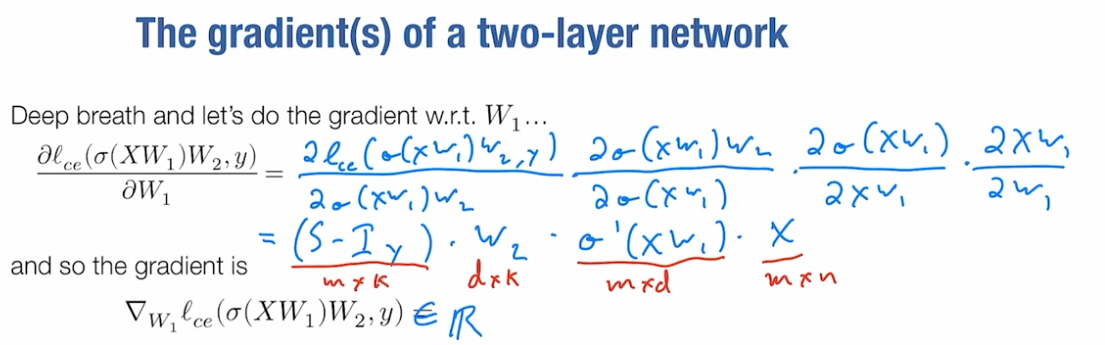
现在是真正有趣的部分。让我们来谈谈矩阵的大小。

所以这个，在之前的基础上，$S-I_y$将会是 $m × k$的矩阵,$W_2$是一个$d × k$ 的矩阵，$\sigma' (XW_1))$将会是$m × d$，然后这个$X$将会是$m × n$,这就是所有东西的大小。

好。那么现在，我们关于$W_1$ 的损失梯度和是和 $W_1$ 一样的尺寸，而$W_1$ 是一个 $n × d$ 的矩阵，它在第一层中将 n维空间转换为d维空间。

那么我们如何从所有这些东西中得到一个$n × d$ 的矩阵呢？

• 好的。首先我们要做的是，这里唯一涉及到 n 的项就是 $X$,所以我们肯定要先对 $X$ 进行转置。现在的$X$是$m × n$, 所以这个转置后的$X$ 将会是$n × m$。

• 其他的内容我们希望它是$m ×d$，实际上我们已经有了$\sigma'(X W_1)$， 它是 $m × d$的,但我们还要将它与其他东西相乘。而$(S-l_y) \cdot {W_2}^T$也是正确的尺寸$m \times d$ 。

  实际上，在这种情况下，我们将这两个$m \times d$的矩阵组合起来的方式是，我们只需取它们的数量积，它们相互的数量倍数。然后以这种方式组合它们。我们想要将它们相乘，它们是相同的尺寸。

• 最后我们能做的就是对它们逐元素相乘，这将得到最终的正确梯度

这是关于 $W_1$的一切的梯度。你知道，再一次，这似乎是我们进行了很多数学推导才得到的结果，对吧？但实际上，要实现这个，你可以用大约六七行 Python 代码编写两层神经网络的随机梯度下降算法。这是非常强大的。

你将所有的时间放在学习自动微分上，这样你就不必再做这些了。

那么现在，假设没有其他人想要构建一个三层网络，我将实际上为一个 L 层网络展示这个的一般情况，尽管在某些时候会涉及一些简化，但事实上，当我们这样做时，情况会变得更简单，而不是更复杂。

Backpropagation "in general"

假设我们现在按照之前在一开始讨论的那样，对于一种任意的前馈神经网络做同样的事情。所谓前馈神经网络(feed-forward neural network)是指每一层的输出是前一层输出的线性函数经过某种非线性激活函数处理得到的。

我们重复这个过程直到 L 层，最终网络的输出就是这种符号表示中的第 L+1 层。好的，那么我们实际上要如何推导$Z_{i+1}$关于$W_i$的梯度呢？

我们来思考一个通用的 L 层网络。

假设我想要计算这个网络对于 W_i的损失梯度，我想要计算损失函数在网络的输出层（第 L+1 层）关于 $W_i$ 的梯度，以更新参数 $W_i$。

我在符号上会更加简洁，为了方便观察，我将把它写成一系列偏导数的形式。

• 注意最后这个项是$\partial Z_{i+1}$

好的.现在有趣的是，如果对$W_{i-1}$，$W_{i-2}$ 等等这些参数都这样操作,你会发现，很多这些项

会一再出现，事实上小于这个 i 的对于$W_i$的梯度都会出现这些项。

这个确实是一个非常非常重要的概念。我们在使用或中间项进行计算时，我们重复使用它们，不仅仅是计算一个梯度，而是计算我们关心的所有梯度。

在神经网络的情况下，我们将为这些项赋予一个名称$G_i$ , 这里我将写出 $G_{i+1}$，因为是从 $Z_{i+1}$ 开始的:

这里真正有趣的是，不同的$G_i$之间存在一个非常简单的关系,比如我有$G_{i+2}$，

$G_{i+1}$只比$G_{i+2}$多一项

我们可以将这个形式化地写成：

现在把$Z_{i+1}$展开，我们将应用链式法则一次，

好的。这就是我们的递归表达式,

因为递归基$G_{L+1}$是可计算的，这样就可以得到每一项$G_i$

但这还是使用我们的作弊符号， 你知道，这些都被视为标量。那么现在让我们谈谈我们如何使用这些运算 ,来计算真正的梯度，而不仅仅是假装的标量梯度，使用我们之前所做的相同的尺寸匹配技巧

Computing the real gradients

好的。那么让我们首先讨论这些 $G_i$ 实际上是什么:

这是依然在把这些量当成标量，但如果我们将其视为一个实际数量，我们实际上在这里计算的是:

所以我们真正想要的是我们的损失函数相对于 $Z_i$ 的梯度,我想强调的关键点是这个东西的大小, $Z_i$ 你会看到 $Z_i$ 实际上有 $m$行（代表数据集的样本数），$n_i$列(代表神经网络第i层的维数)。所以我们损失函数关于 $Z_i$的梯度也应该具有相同的大小,它应该是 $m \times n_i$。

现在把以下的$G_i$表达式转化为矩阵的表达

$G_{i+1}$和$\sigma'(Z_iW_i)$的大小是$m \times n_{i+1}$,而$W_{i}$的大小为$n_{i} \times n_{i+1}$

考虑矩阵的大小以后得到

现在我们已经有了 $G_i$ 的反向迭代。

但我们更需要的是损失函数相对于参数$W_i$的梯度,大小为 $n_i \times n_{i+1}$

非常类似于我们过去的表达式，与过去的表达式唯一的区别,是因为我们现在是相对于$W_i$ 求导。考虑矩阵的大小，则得到

在我们实际上已经做完了你需要做的一切，来计算任意 L 层网络的所有梯度。

我已经告诉你如何计算实际梯度，不仅仅是理论梯度，还有这些不同矩阵的实际大小。很多时候，你会看到神经网络的梯度以逐元素的方式写出，只是因为标量容易处理，你会有不同项$W_i$的导数，但实际上没有人会真正地以那种方式实现它。

因为每个人都在使用自动微分,但即使你真的从头开始实现反向传播，我稍后会讲到反向传播是什么，你也会始终使用矩阵运算来实现它。

你知道，我们在使用奇怪的大小以及这种非常诡异的方式来匹配它们,我承认这是一种诡异的方法，但是我们之所以这样做，确实有原因。学习这些东西实际上是如何工作的，以及以我们实际上会实现的方式工作，要比现在派生出每个单独的表达式, 以一种实际上没有人会真正实现的方式好得多。

Backpropagation: Forward and backward passes

所以，经过上述的讨论，我们的算法最终形式是什么样的？

现在，这种计算梯度的方式被称为反向传播，对吧？而反向传播通常被分为两个不同的步骤：

• 网络的前向传递，计算 $Z_i$ 项，

• 网络的后向传递，计算 $G_i$ 项。

让我们更加明确一些，我们是如何计算前向传递和反向传递的，以及如何计算所有这些梯度。

Forward pass

首先，我们将第一层初始化为输入层，就是一种约定俗成的做法。我们将第一层$X$设置为输入层。这样我们就可以在后续层次中使用相同的符号表示。然后，我们使用迭代方式计算 $Z_{i+1}$ 的值，即从 1 到 L

顺便提一下，我之前强调过，非线性函数在不同的层可能是不同的，而且通常最后一层甚至没有非线性函数，只是一个线性层而已。但这只是细节问题，实际上你可以根据需要进行设置。

好的，这个计算实际上就是网络的前向传递，或者称为反向传播的前向传递。后向传递有时候也被称为反向传播，尽管你可以把前向和后向传递都称为反向传播，其实，你如何称呼反向传播甚至自动微分都有点奇怪。

我认为即使是 Tianqi 和我在这方面的术语上也略有不同。所以要知道并没有单一的定义，但除此之外，可以说反向传播是计算梯度的方法。

backward pass

反向传播的后向传递的作用是首先初始化最后一个反向梯度，即与最后一个单元本身相关的损失的梯度:

这就是第一个项$G_{L+1}$。

然后，按照我们在前一页中精确推导出的方式对 G_i 进行后向更新。因此，这就是这些项的更新。最后，你要从 L 开始，以逆序的方式从 i=L 到 1 进行操作。在执行此过程时，你当然也可以计算梯度，这正是我们在上一页中对参数所做的。

重要的是要记住，在一次前向传递和一次后向传递中同时计算所有参数。因为我们可以使用这些 $G_i$ 项和 $Z_i$ 项来计算所有需要的参数。但为了做到这一点，我们需要在这个过程中进行一些缓存，也就是计算这些$G_i$ 项以便重复使用它们，而不是从头开始形成它们。

因此，从更广泛的意义上说，反向传播只是链式法则和中间结果的intellectual caching这就是反向传播的含义。

现在，我想强调一下这一点，就是为了计算相对于 $W_i$ 的梯度所需的形式，它包含了 $Z_i$ 和$G_i$ 两个项。这意味着为了计算这个梯度，我们可以在后向传递过程中沿途进行计算，但我们必须存储 $Z_i$ 的值。我们不能丢弃前向传递中的任何中间项，而是必须保留它们，以便在后向传递过程中使用它们来计算一部分后向梯度 。

• 虽然从完成一个前向传播加上一个反向传播的角度来看，这种方法是高效的，但实际上它的复杂性是单个前向传播的两倍。在某种程度上，它的内存效率较低，因为我们必须在整个过程中保存所有的中间项。

• 如果我只是想计算输出(即只有Forward pass)，那么一旦计算出$Z_(i+1)$，我可以丢弃$Z_i$，但在反向传播中，我不能这样做。

在这个前向和后向传播中维护中间元素的概念对于反向传播至关重要，这成为反向传播的主要权衡之一。它允许更高效地计算梯度，但可能会增加内存存储的成本。这只是后续内容的预览，请记住，当我们讨论反向传播的效率时，它在计算上非常高效，但至少从表面上看，它确实会增加一些内存开销。

A closer look at these operations

实际上，这就是多层神经网络的通用反向传播的真正矩阵形式。我认为公正地说，大多数讨论反向传播的机器学习课程通常就到这里。他们会讲解如何推导反向传播，也许还会谈到卷积，但他们甚至不会详细讲解如何为卷积推导反向传播。他们只是讨论卷积的前向传播，并假设一切都能解决。当谈论实际的反向传播时，大多数课程在那里结束，甚至可能连矩阵形式都没有涉及，但对于我们来说，这只是一个开始。实际上，在本课程的后续内容中，我们将不再使用这种方法。

因此，在我们再也不涉及这些内容之前，我想让你再深入思考一下在反向迭代中实际上正在发生的事情。为了计算对$W_i$的梯度，当然，现在我将其写成偏导数的形式，但实际上它是一个梯度。我们需要做的是将$G_{i+})$与各个项相乘，当然，利用链式法则进行分解。

基本上，我们需要将其乘以这些只涉及第i层$Z_{i+1}$导数的项。从某种意义上说，我们可以将其视为第i层的任务是什么。首先，第i层必须计算自己。它必须知道如何计算第i层。但它还有责任去计算第i层的前向传播，也就是计算自己$Z_i$。它还需要将传入的反向梯度$G_{i+1}$，乘以自己的导数，即$\frac{\partial Z_{i+1} }{\partial W_i}$。我指的是一个很大的雅可比矩阵，暂时忽略这个。

一般来说，为了适应反向传播框架，任何层都必须能够将传入的反向梯度与自己的导数相乘。实际上，这是一个非常常见的操作，有自己的名称，被称为向量雅可比乘积。这个术语实际上很误导人，因为G_i实际上并不是一个向量。但它的真正意思是，如果你将整个事物看作一个向量，并将这个事物看作多元微积分中的雅可比矩阵，那么将这个东西乘以这个东西的操作就被称为向量雅可比乘积。非常有趣的是，这个过程可以变得更加模块化和通用。

下一节课，我们将介绍这个过程，可能不是完全通用，但在接下来的几节课和作业中，你将学习到这个过程，这也是自动微分的内容，将完美地避免了所有这些令人困惑的数学和手工应用链式法则的需要。所以你必须做一次，最好亲自进行一次手动推导多层神经网络的反向传播。然后将其搁置一边。下次我们开始讨论自动微分，或者说我们如何在实践中做到这一点。