Lec4.1 How does differentiation fit in machine learning

首先，让我们首先回顾一下为什么我们需要进行自动微分以及不同的微分方法。然后，在讲座的第二部分，我们将介绍一种主要的方法，即反向模式自动微分，这种方法在现代深度学习框架中被广泛使用。

那么我们从第一个开始。自动微分如何适用于通用的机器学习工作流程呢？如果回想前两节课，我讲述了机器学习的基本要素，或者你可以考虑机器学习算法。通常情况下，我们需要从几个角度来思考。首先，我们需要考虑假设类别（hypothesis class），也就是针对给定的输入x，如何得到预测值。在前几节课中，我们讨论了多层感知机和单层感知机算法作为正常情况下的假设类别。在接下来的讲座中，我们将讨论不同的假设类别，如卷积神经网络(convolutional neural networks),Transformer和generative neural networks，它们可以将给定的输入转换为预测。当然，对于给定的假设类别，仍然有一些未确定的因素，具体而言，每个假设将由一组参数$\theta$进行参数化，我们需要从训练数据中学习一个好的$\theta$。因此，机器学习中的第二个要素通常是损失函数。损失函数定义了对于给定的假设类别和参数$\theta$，我们的预测有多好。通常情况下，我们使用训练数据集来衡量。因此，我们将试图找到一组$\theta$，使训练数据集上的损失函数最小化，然后我们将使用学习到的参数$\theta$来对未来的数据集进行预测。损失函数是衡量我们的模型性能的元素。最后，对于给定的损失函数，我们仍然需要能够找到一个优秀的$\theta$，使得损失函数最小化。这就是第三个角度的作用，也就是优化方法。大多数机器学习优化算法实际上都采用随机梯度优化的形式。我们会尝试计算损失函数相对于参数$\theta$的梯度。梯度函数是一个指导方向，通常它会使损失函数稍微增加一点，我们的目标是减小它，对于小步长，我们会朝负梯度方向迈出一小步。我们使用的大多数方法通常也被称为随机梯度方法，这意味着我们不是尝试计算整个数据集上的梯度，而是从数据集中选择一个小批量样本，然后直接朝着该小批量上计算的梯度方向迈出一小步，这通常被称为随机梯度方法(stochastic gradient method)。

当然，根据具体的更新算法，更新规则可以有所不同。在这种情况下，我们展示了随机梯度下降的基本形式。在后续的讲座中，我们还将讨论其他更新方法，包括动量法和自适应梯度法等。但在所有这些情况下，我们需要解决的核心问题是如何计算损失函数关于$\theta$的梯度。这是几乎所有机器学习算法中用于学习给定数据集的关键部分。

幸运的是，现在我们不再需要手动计算梯度，因为有许多工具可以自动完成这个过程。老实说，对于你们现在处理的复杂模型，手动推导梯度几乎是不可行的。因此，我们的目标是讨论一些能够以更自动、更实用的方式获取梯度的方法。

Symbolic differentiation

Computational graph

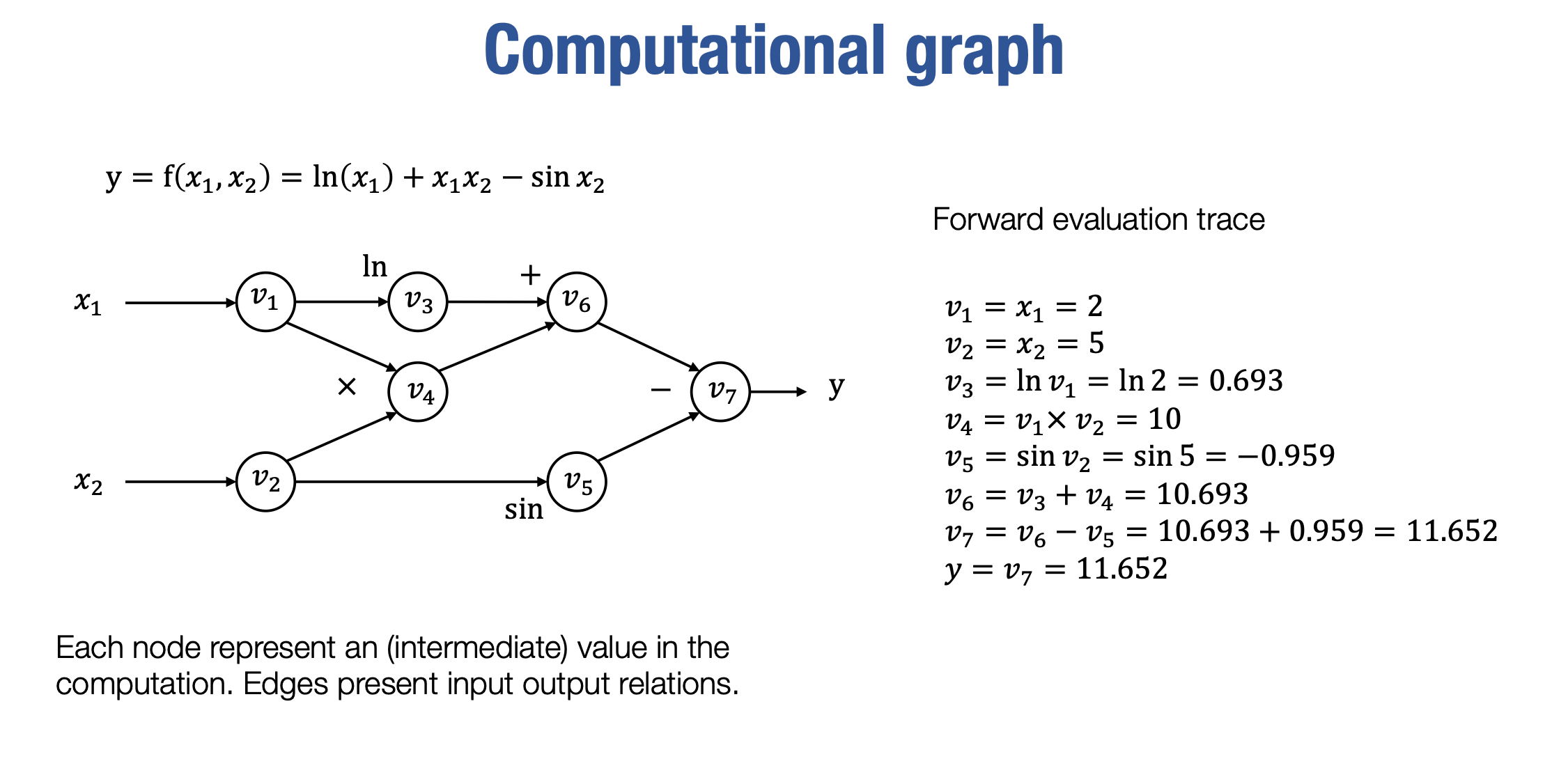
现在让我们介绍第一种自动微分方法, 但在此之前,让我们先介绍一些在本课程中将要使用的基本工具。如果你之前使用过一些深度学习框架，你可能已经听说过它们，被称为计算图（computational graph）。

计算图几乎是所有机器学习框架的核心，对于我们推导自动微分方法来说，它也是一个重要的工具。实际上，计算图是一个用于表示对某个函数进行计算的有向无环图（directed acyclic graph）。例如，silde展示了一个表示特定计算的计算图。

当然，对于单个计算而言，可能有不同的计算图方式，因为如果你能计算三个元素 A、B 和 C 的乘积，你可以先将 A 和 B 相乘，然后再乘以 C，或者你可以将 B 和 C 相乘，这将对应两个计算图。

计算图还在某种程度上指定了执行顺序的一些信息，计算图中的每个节点表示一个中间计算过程。

例如，这个

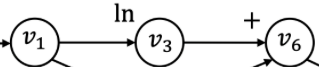
特定节点表示了这个对数计算，它接收$v_1$ 的值作为输入，并输出 $v_3$ 的值，这个值被输入到计算 $v_6$中。因此，每个节点代表计算中的中间值，而边表示这些计算之间的输入输出关系。每个计算图中的计算节点都有输入地址，表示它们的输入，而输出地址表示它们的输出去向。

让我们沿着左边的计算图，逐步进行手动计算这个计算图,我们这样做是因为这将对我们将来推导自动微分的情况有所帮助。

在这个特定的例子中，假设我们对2和5的路径（即$x_1=2$和$x_2=5$）感兴趣，现在按照拓扑顺序遍历这个图。

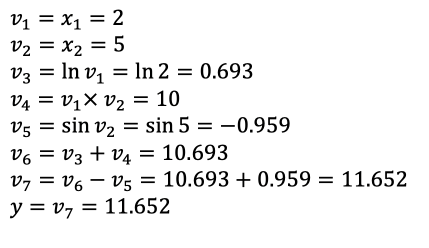
最后得到结果 y，对于计算图，你可以将值放在输入侧，然后按照拓扑顺序遍历计算图。对于每个节点，你尝试获取已经计算好的输入值，因为我们按照拓扑顺序遍历，然后，我们计算该节点的输出值。在遍历整个图之后，你就能得到最终的输出值。

这是大多数深度学习框架用来表示计算的工具，同时，它也是推导自动微分的一个非常有用的工具，

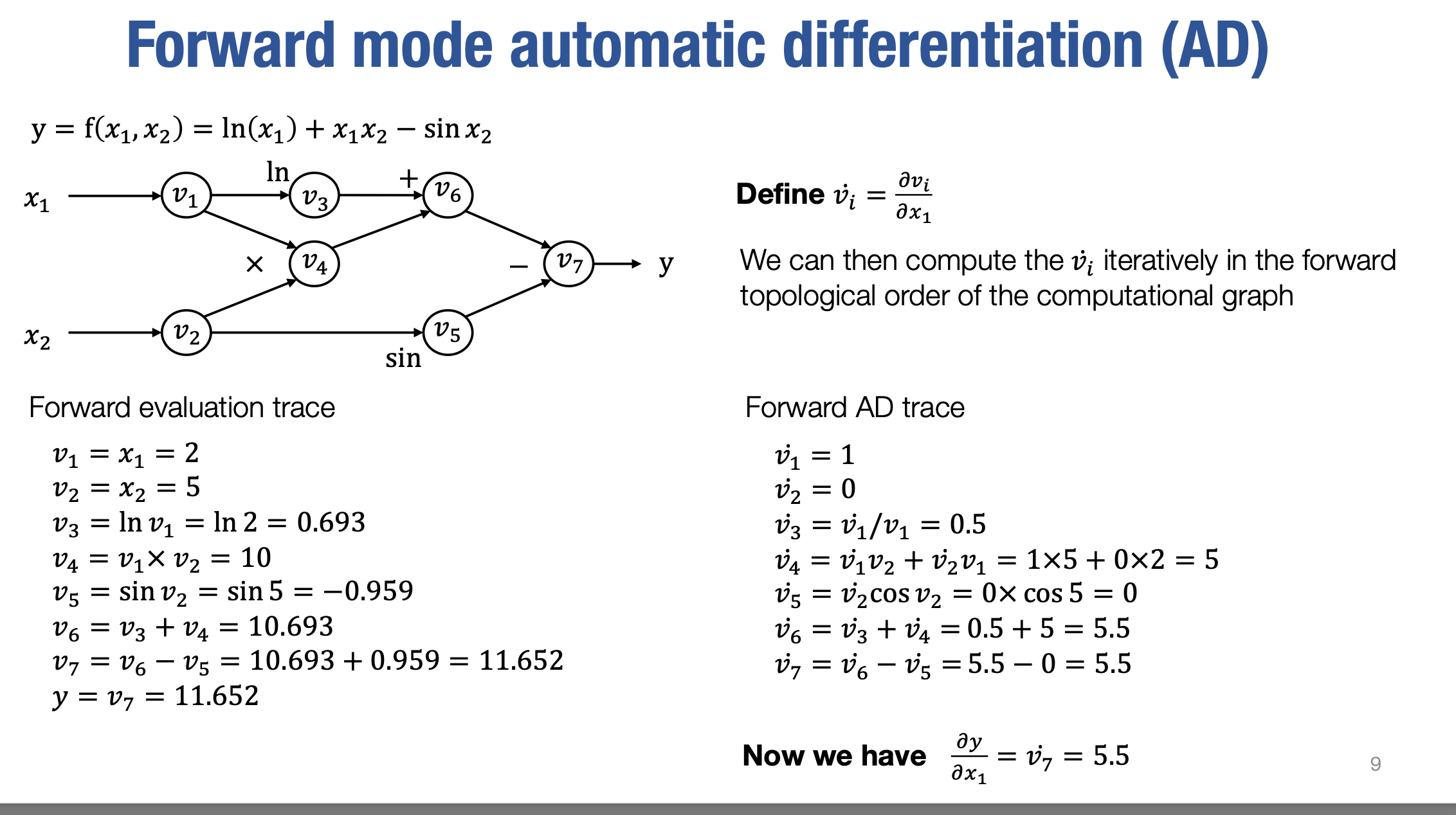
现在我们准备介绍第一种自动微分方法，它被称为前向模式自动微分(forward mode automatic differentiation )。

假设我们对每一个中间值相对于第一个输入（即$x_1$）的偏导数感兴趣，我们将递归地为计算图中的每个节点推导出这个值。

首先，让我们看一下$\dot v_1$是什么, 根据定义我们知道

我们知道$v_1$等于$x_1$，所以$\dot v_1$实际上等于1。类似地，对于$v_2$，我们知道$v_2$等于$x_2$，所以与$x_1$无关。因此，在这种情况下，$\dot v_2$等于0。接下来，应用链式法则，我们得到每个中间值关于$x_1$的偏导数

(是$x_1=2$ $x_2=5$时中间值关于$x_1$的偏导)

最后，我们可以发现，在遍历完计算图中的每个节点之后，我们将得到$\dot v_7$，即最终节点$x_1$的偏导数。

所以我们可以发现，为什么我们称之为前向模式自动微分：

• 我们从最开始的节点开始推导，如果开始的节点(如$v_1$)等于我们想要对其求导的输入参数(如$x_1$)，那么梯度值为1；否则，梯度值为0。

  （偏导和梯度有点混用，明白意思即可）

• 对于每个中间的计算图节点，我们尝试做

  $$\dot v_i=\sum_{j\in input(i)} \frac{\partial v_i}{\partial v_{j}}\dot v_{j}$$

  通过进行递归的计算，只要我们知道所以输入节点的$\dot v_i$，就能够计算出当前节点的$\dot v_i$点，依此类推。

• 在遍历整个计算图之后，你将得到所有节点的$v_i$点。

在这种情况下，这就是前向模式自动微分。

另一方面，如果你想计算神经网络的梯度,你会发现前向模式自动微分仍然存在一些限制。

具体而言，如果你有一个接受n个输入和k个输出的函数，当n较小而k较大时，前向模式自动微分非常有效，因为它允许我们能够一次性计算相对于一个输入的梯度值。因此，如果n较小但函数有很多输出，我们可以通过一次遍历来获取相对于该特定输入的所有输出的梯度值。

然而，如果我们有较多的n个输入参数，为了获取梯度，我们需要运行n个前向自动微分遍历来获得相对于每个其他输入的梯度。

在深度学习中，我们通常关注的是一个输出标量。因此，我们对一个标量输出感兴趣，其中损失函数是一个标量，而输入参数很多。

因此，为了解决这种类型的问题，我们需要一种不同的方法。这就是我们今天讲座的第二部分将要介绍的方法，称为反向模式自动微分。