Lec3.2 Neural network

Neural network/ deep learning

现在，总的来说，这个术语“神经网络”，是一个很棒的术语，对吧？我会说，机器学习非常擅长于为我们的算法想出巧妙的名称，不仅仅是神经网络，还有类似于梯度爆炸之类的东西。我猜这些名字来自于统计学，这些都是非常棒的名称。它们听起来很酷。神经网络也不例外，我第一次听说神经网络，可能是来自《星际迷航》之类的东西。它来自于大脑的概念，但神经网络到底是什么？

好的，为了预览接下来要说的话，我要说的是，它与大脑或类似这样的东西没有关系。至少在它的当前形式下，这里没有非常明显的联系。相反，神经网络所指的是一种特定类型的假设类，我们在机器学习中使用它。这就是神经网络。

它是一种特定形式的假设类，并不是通过类似大脑学习或模拟大脑这样的方式进行分类的，它的特点是具有多个参数化的微分函数，我们称之为层，这些层组合在一起，从输入映射到输出。

现在，正如我所说的，这个术语的确源于生物，但是此时，任何上述类似的函数都被称为神经网络。我实际上不想忽略生物启示，因为神经网络的许多发展确实来自于思考生物过程中的类比。而且，神经网络的许多创新，实际上是从思考大脑如何工作开始的，对吧？事实上，大脑就是一个存在证明智能系统的例子之一。

但是，我还需要强调，目前在实际工程中，我们所开发的实际上的网络和我们目前所知道的大脑之间的联系非常微弱。我真正想强调的是神经网络是组合可微函数的观点，

因为从工程的角度来看，这就是神经网络。

现在，深度网络这个术语只是神经网络的同义词。而深度学习则只是使用神经网络假设类进行机器学习的意思。尽管在深度学习的术语中存在一些争议，但我认为我们需要停止假装神经网络必须具有某些深度才能被称为深度学习。

许多人将使用两层神经网络作为深度学习方法，我认为这是可以接受的。在学习方面，区别是否是深度学习在于是单层网络（即线性假设类）和还是超过单层的网络。

虽然这个术语曾经存在一些争议，但我认为“深度学习”一词通常指的是使用多层神经网络作为机器学习的假设类。这实际上并不是... 尽管在某些情况下这可能是错误的，但在许多应用中，我们实际上使用了相当深的网络和神经网络，所以“深度”通常是一个合适的限定词。但是，希望这至少让人们了解我如何在这里使用这些术语，以及它们在实践中通常如何使用，即使有些人会不同意并说，在真正的深度学习之前，必须有这么多层。我认为在这里没有达成共识，所以我们只称所有神经网络为深度学习。再次强调，这是一个非常好的营销术语，对于机器学习来说非常好。

The "two layer" neural network

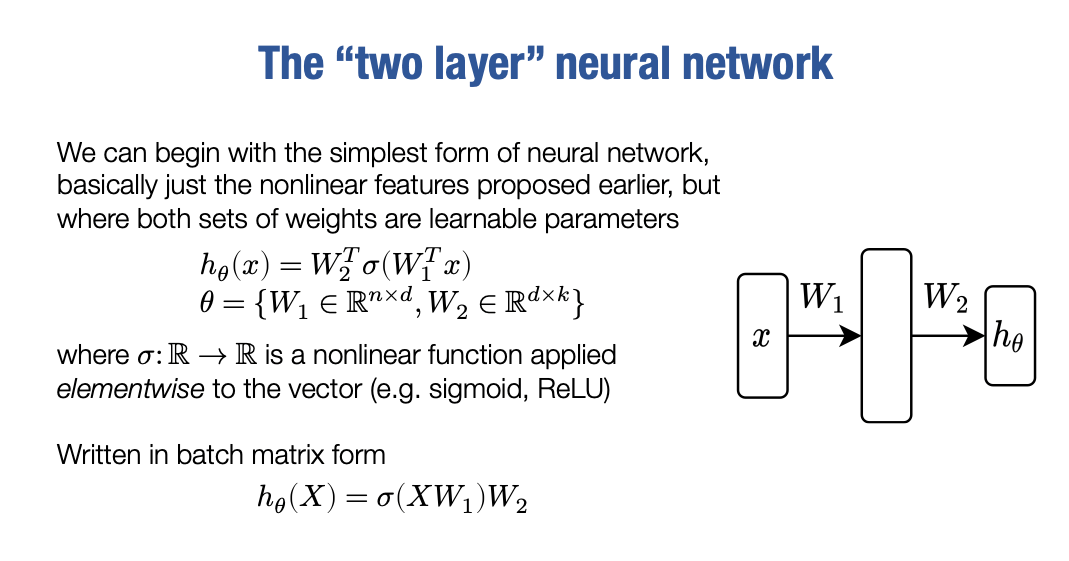
我们来到开始介绍的假设类，也就是一个两层神经网络。

而这个两层神经网络基本上就是我们之前提出的非线性特征的集合。如果你看一下这个假设，我们定义在这里的是一个非线性函数$\sigma$应用于输入$x$的线性变换的线性函数$W_1^T(x)$, 得到非线性的特征向量

• 从现在开始，这更为标准化，我们不会再有一个外部线性参数$\theta$和一个内部线性参数$W$。事实上，因为$\theta$通常在某种程度上指代了网络的所有参数，我们现在要做的是将$\theta$改写为$W_1$和$W_2$这两个参数的集合。所以，这个表达式会和上一次看到的略微有所不同，因为在这个公式里$W_1$和$W_2$都是参数，是我们将要优化以解决机器学习问题的可调参数。我们把它们都视为我们的参数集中的一部分，然后把$\theta$看作我们所有参数的集合。

• 此外，正如我之前所说的，$\sigma$只是应用于向量的某些非线性函数。有时人们会将$\sigma$特别指代为一种非线性函数，即Sigmoid函数，但实际上在这种表达式中，它可以表示任何东西。它可以表示ReLU、Sigmoid、正弦函数、tanh函数，实际上什么都可以。我只是用它来指代任意的非线性函数。

  有时我们会使用这个图像来表示这个网络。

  

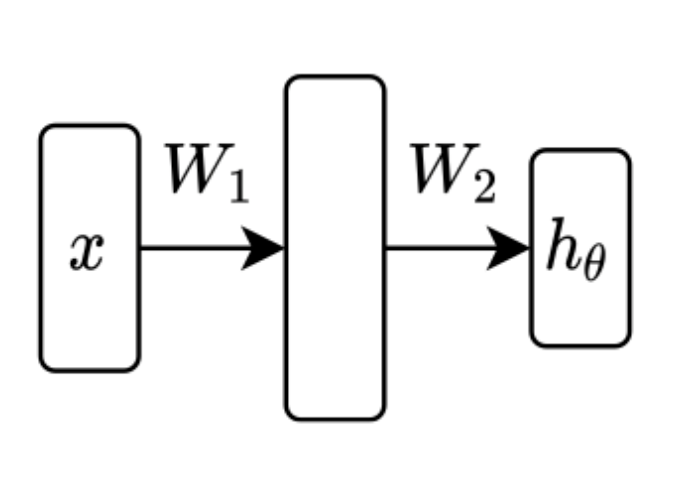
  我们认为这个网络通过$W_1$和$\sigma$将$x$转换为另一组特征，然后使将其转换为我们的输出。事实上，当我们更加仔细地提取这些特征时，对于网络的不同层次的不同特征值，我们将引入术语。但在这里，我们只需要显式地写出这个式子。

  $$h_{\theta}(x)=W_2^T \sigma(W_1^Tx)$$

  实际上，我们很快就会放弃这个式子，而始终将其以批处理形式写出：

  $$h_{\theta}(X)= \sigma(XW_1)W_2$$

  请记住，$X$在这里将是一个$m \times n$矩阵，其中$m$是我们训练集中的示例数量或批量大小，也许我们会用$B$表示训练集的子集。

  让我们检查一切维度是否合理。$X$将$m\times n$，$W_1$将是$n \times d$，因此整体$XW_1$是$m \times d$，$\sigma$因为我们仅仅是将$\sigma$逐元素应用于矩阵，因此还是$m \times d$。然后，$W_2$是$d \times k$，最终结果是$m \times k$。这将是我们数据集中所有示例类别的逻辑预测。

Universal function approximation

好的，现在在我深入探讨更复杂的神经网络形式，以及反向传播和如何计算梯度之前，我想先稍微跑个题，谈谈神经网络的一个性质，我们其实已经有足够的知识给出一个基本证明。

我将仅对一维情况进行说明，也就是输入和输出都是标量值的神经网络，但是一般的定理并不会更加复杂，适用于任意维度的输入。我们要证明的是一个两层神经网络（就是你在前一页看到的那个形式），事实上即使是更简单的形式，也就是我稍后会提到的，都可以称为是一个通用函数逼近器。

这意味着，一个两层神经网络能够任意精确地表示一个定义在某个封闭区域上的函数。这个区域需要是一个有限的输入子集，也就是有限的输入空间。但是在这个有限的输入空间中，我们可以构建一个两层网络或者说一个单隐藏层网络 $\hat{f}$，可以任意逼近任何平滑函数 $f$。

单隐藏层神经网络通常被定义为一种具有输入层、一个隐藏层和输出层的神经网络，因此可以看作是两层神经网络。输入层接受输入数据，隐藏层执行计算并学习特征表示，输出层生成最终的预测结果。

具体来说，如果我们选择一些误差逼近量$\epsilon$，那么在这个$\epsilon$ 的基础上，我们总可以找到一些神经网络，即一个两层神经网络，也就是一个单隐藏层神经网络，使得我们的真实函数与逼近函数之间的差异在任何地方都被 $\epsilon$ 限制。这意味着，两层的神经网络可以以任意精度逼近任何函数。

你可能会认为，线性函数具有一定的能力，但我们只是引入了一个稍微复杂一些的函数，对吧？我们只是从线性函数转移到了这个函数。这似乎不比线性函数强多少，但事实证明它确实更强大。实际上，它可以表示任何函数。而线性函数当然只能在$n$维空间中表示直线或平面。

这是一个非常强大的陈述，但同时我也想强调这个所谓的“特性”其实并不是神经网络的伟大之处。在另一种意义上，很多函数都有类似的特性，比如最近邻、多项式和样条逼近等等。虽然这些函数也有通用逼近的能力，但人们并不太关心它们，因为它们并不像神经网络一样被广泛使用。因此，这个特性并不是神经网络如此强大的原因，它实际上是完全不同的东西。多项式有一定的局限性，因为它们只在某些数量上是通用逼近器，而最近邻或样条逼近等函数则更加通用。

好的，那么这里是基本的想法。

现在假设我们有一个函数$f$,这将是一个一维函数，对吧？所以在x轴上是$x$，在y轴上$是f（x）$，我们要做的是首先在许多点上对该函数进行采样，我将在样本点上使用不同的颜色，我们要在许多不同点上对该函数进行采样，在这个有限集D上进行逼近，在这个空间中我们将构建一些基本的网格。

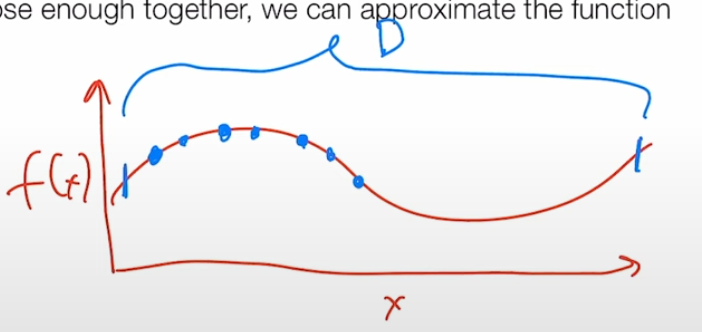
• 在1D中，这只是一组点，在2D中将是一个网格，在3D中将是N维网格，要明确的是这里会有很多点。

在1D情况下，我们接下来要做的是构建一个线性函数，它将在所有这些点之间进行步进，这实际上就是我们对该函数的近似$\hat{f}$。我们将构建这种线性插值,由于函数是连续的，我们实际上可以用这种分段线性近似,任意地接近底层函数 。

首先，你应该立即想到，我们正在形成一个线性样条近似，这当然意味着线性样条具有所有相同的通用函数近似特性。

线性样条近似是一种基于插值方法的函数逼近技术，它将函数表示为一系列线性函数片段的组合。对于一个一维的函数，我们可以通过对函数进行插值得到一组数据点，并且根据这些点构造一个线性样条函数来逼近原函数。线性样条函数是一些线性函数的拼接，每个线性函数片段都通过两个相邻的数据点进行插值得到。在每个数据点处，这些线性函数片段的斜率相等，使得整个函数的导数连续。线性样条函数可以在一定程度上近似原函数，因为线性函数片段之间的连接点数量越多，近似的精度就会越高。

但在这种情况下，我们将展示一个神经网络，也可以表示这种线性样条，特别是一个使用ReLU运算符的神经网络。

事实证明，要形成一个可以做到这一点的神经网络，你需要隐藏单元（我们有时也称其为特征向量）的维数，与我们拥有的样本点数量一样大。

也就是说，实际上近似这个函数的神经网络的大小可以任意变大，这是一个不错的特性，但不太实用。好的，那我们怎么做呢？如何构建一个能够近似这个线性样条的神经网络？

Universal function approximation

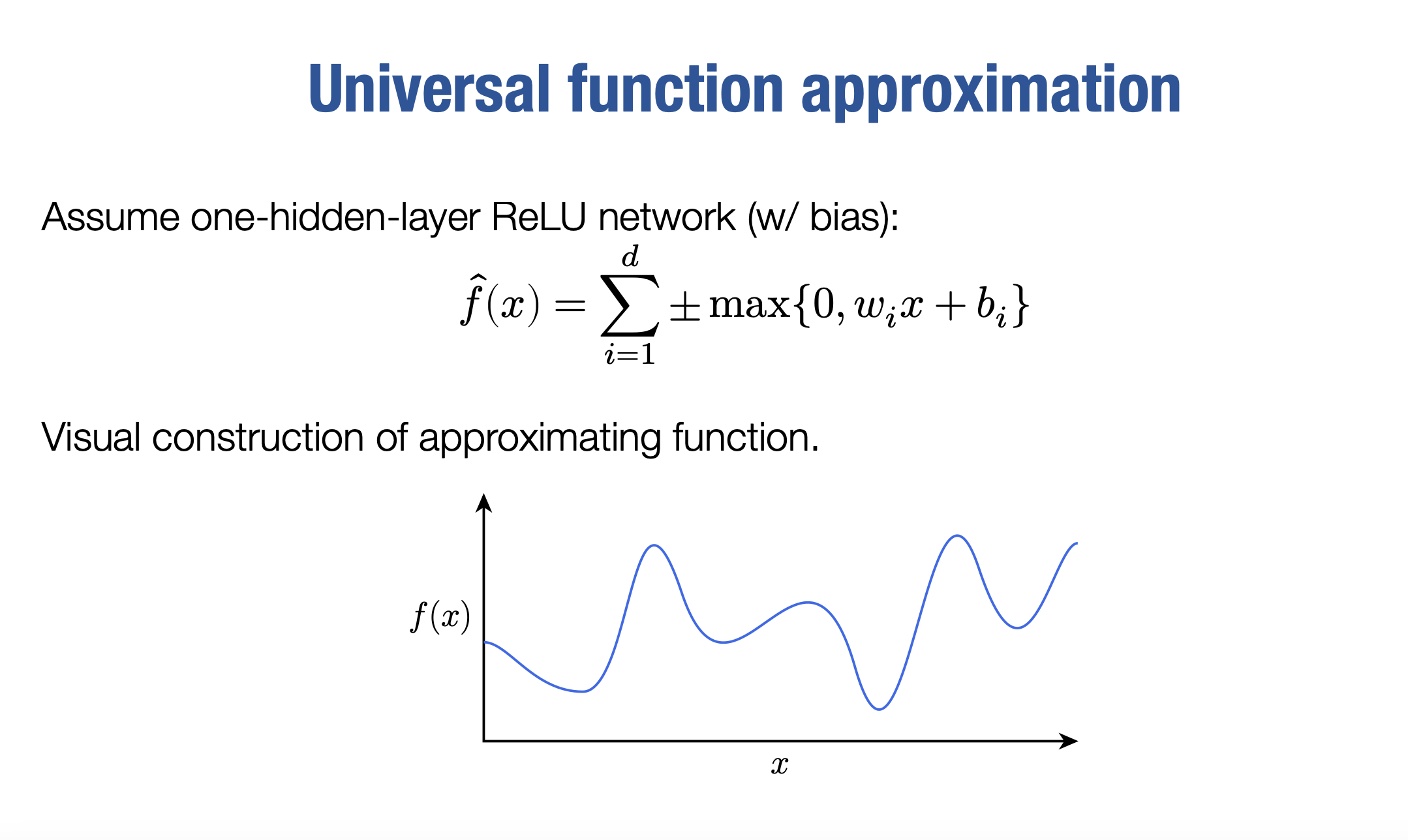
现在，我们的做法是，我们将使用一个具有一层隐藏层的ReLU网络。我们将在这里使用一个偏置$b_i$。

我之前没有提到的一件事是，我们之前使用的函数实际上不包括我们所谓的偏置项$b_i$。当我们开始谈论更通用的神经网络时，我们将回到这个问题，但在这个讲座中，我们大多数时间都不会使用偏置项。因此，我们只是将我们的特征作为输入的线性函数，而不是添加这个我们称之为偏置的项。但是对于这个证明，我们实际上确实需要一个偏置项。

好的，因此我们的函数$\hat{f}$将是一些单独ReLU函数元素的总和：

请记住，现在讨论的输入是x是实数, 而不是向量。在我介绍如何构建这个函数$\hat{f}(x)$之前，我想先介绍这个函\实际上长什么样子？这个函数实际上长什么样子？好的，内部的函数基本上是像这样的函数。

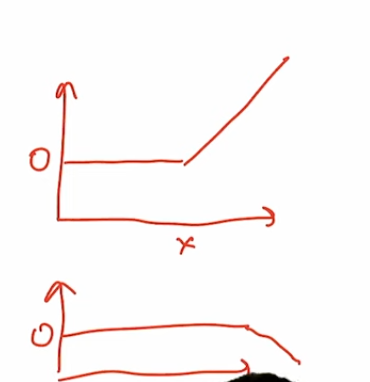
这些函数看起来是常数函数，直到某个点，因为这里有零，所以到处都是零。在某个点之前是零。然后在那个零点之后，基本上每当这个内部项是负数时，这些函数就为零。然后在那之后，它们有一些线性斜率，这个线性斜率可以上升或下降。顺便说一下，这就是我所说的加或减的意思。我们让函数......所以函数可以像这样，也可以像这样。我应该把它们分开写出来，否则有点混淆。因此，当X低于某个值时，它是零和左半部分，然后突然上升，变成这两种情况之一。通过控制偏置和斜率，我们可以控制在X轴的哪个位置从零变为正或负。但是基本上，在内部的函数中，它们看起来就像这两种情况之一。

好的，那么我们接下来要做什么呢？实际上看起来是什么样子？那么我们如何用这样的元素来逼近这样的函数$f(x)$呢？

好的，我们可以做的一件事是，首先，我们可以取我们的函数，我们想在这个区域内逼近，我们可以从一个常数函数开始。而那个函数实际上只需要在第一个函数中$w_i$设置为零，将$b_i$设置为正数，因此假设，你知道，我们在这里是零，零在这里。因此，这整个函数，至少在起始点，是正的。如果不是，顺便说一句，这很容易修复。这不难做到。但为了简单起见，让我们假设如此。

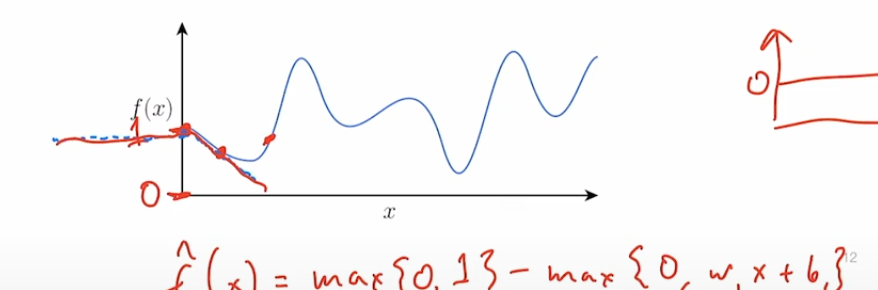
• 我们最初的起点是常数函数

  $$\hat{f}(x)=max\{0,1\}$$
• 接下来，我们会选择另一个点，然后将一个函数加到$\hat{f}(x)$中，使得在该点之前这个函数的值为零，之后为负数，并且负斜率为函数$f(x)$在该点的导数

  $$\hat{f}(x)=max\{0,1\}-max\{0,wx+b\}$$
• 我们可以重复这个过程，每次选取一个新的点，并将一个新的函数添加到$\hat{f}(x)$中。最终，我们的函数将穿过所有的点。这个方法可以用来近似一维函数，即使是非线性的。我们可以通过添加这个非线性函数来逼近各种连续函数。这种方法虽然有一些局限性，但它展现了我们在只给特征向量添加一个线性函数就有很强的能力。

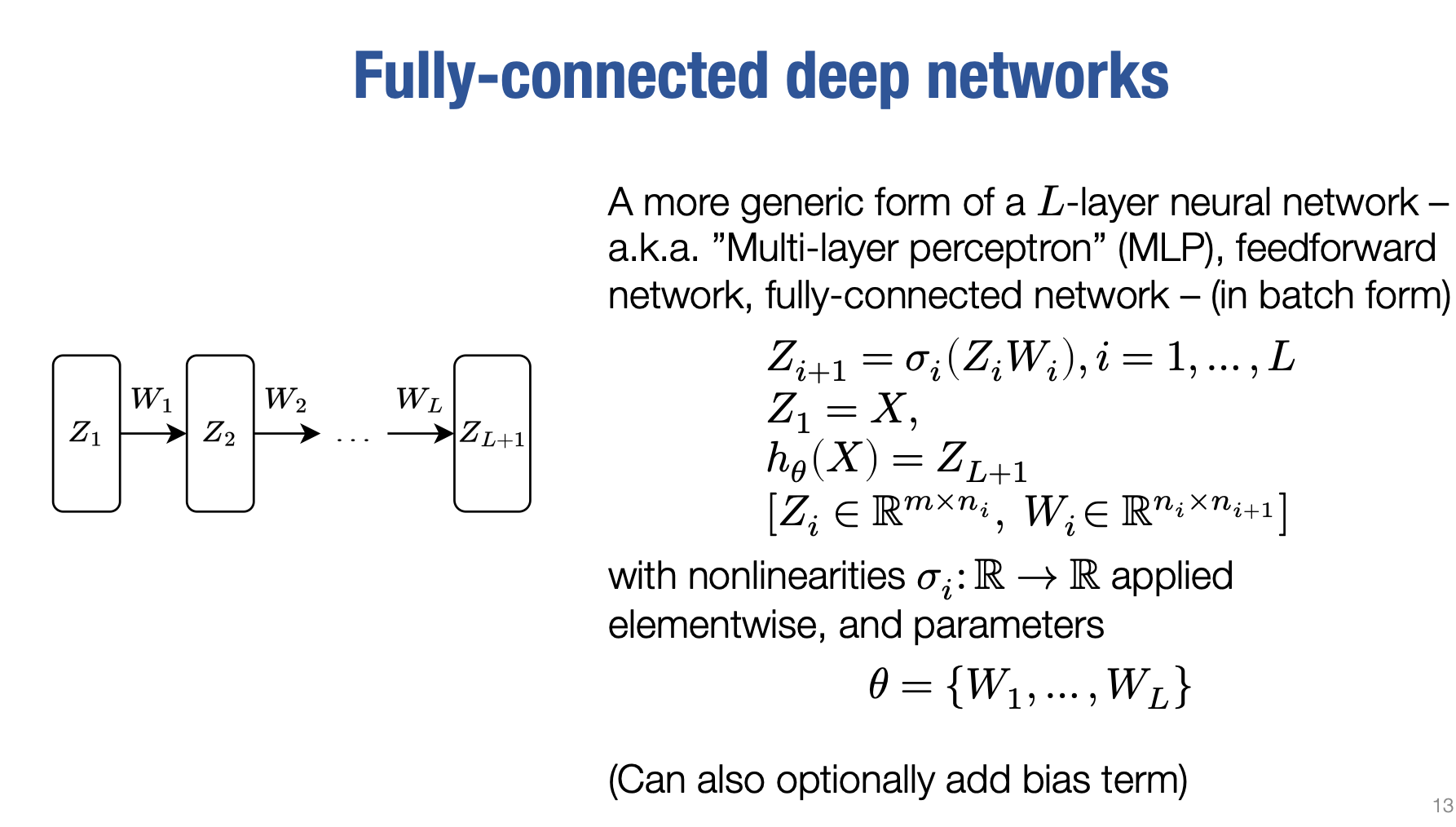
好的。这一点解决了，现在让我回到我们实际使用的神经网络，然后最后谈一下反向传播。因为我们很快将要使用的不仅仅是这个两层网络，而且要考虑更通用的$L$层网络形式，这里的$L$表示网络中层数的数量。

输入层$Z_1$是第0层,因此这是一个$L$层的神经网络

虽然一开始我强调深度学习实际上是指具有神经网络的任何机器学习，但现实是，大多数我们今天使用的深度学习都是基于不仅仅有一个隐藏层，也就是不仅仅有两层用于输入和输出之间的转换。我们通常将其写成多层感知器或MLP的最简单形式，这实质上只是一系列相同转换的顺序应用。

我之所以对此感兴趣，是因为我们稍后在讨论反向传播时将使用这种术语，而且思考这些网络时值得考虑，不仅仅是一种固定函数，恰好具有两层，而是在整个网络中顺序应用的迭代。

• 这里我们要定义一个$L$层网络，其中函数的输入是$X$。

• 这只是我们的输入矩阵，我们将其直接称为$Z_1$。

• 这些值,从$Z_1$开始往后，我们将它们称为层。无论是指激活还是中间特征，有时候我会避免使用层这个词，有时候也会称之为神经元。这些都是网络不同阶段形成的中间特征。现在，"层"可能是个不恰当的术语，但我还是会使用它。有时也被称为隐藏层，但是对于这些术语，用词很多，我可能不应该只使用层这个词，

• 因为层有时也可以指将一个事物转换为下一个事物的实际权重。我应该尽量使用"隐藏层"或"激活"这样的术语，但这些术语都用于描述这些事物。实际上，更准确地说，我可能不应该称$Z_1$为层，因为$Z_1$通常不是一层。我应该称其为网络的中间层、激活层、神经元或隐藏层。

那么这是什么样的网络呢？什么是L层网络？我们通常将其定义为第一层等于输入，对吧？所以这是最简单的事情。为了方便书写，我们希望为每个层使用相同的术语。所以我将称之为或定义$Z_1$等于$X$。

而$Z_i$将成为这个网络或隐藏层的层,这个网络的真正关键是这个方程：

这意味着网络的i+1隐藏层将等于$Z_i$乘以我们的矩阵$W_i$，然后应用非线性的函数。基本上，这只是一个通用化的概括，我们称之为一个两个隐藏层的网络，我们在之前看到的两层网络到L层网络。所以我们将输入转换为一种特征，然后将其转换为另一种特征等等。

我们将在接下来的几秒钟内讨论为什么这可能是一个好主意，但这是深度学习中人们经常使用的形式。现在，为了完整起见，我想谈谈它们的大小。哦，我还应该提到这里考虑的实际输出或假设类别将只是$Z$，即L+1层。我会在术语上保持一下。

顺便说一下。有些人会说L层网络从$Z_1$到$Z_L$，因此将具有L-1组权重。

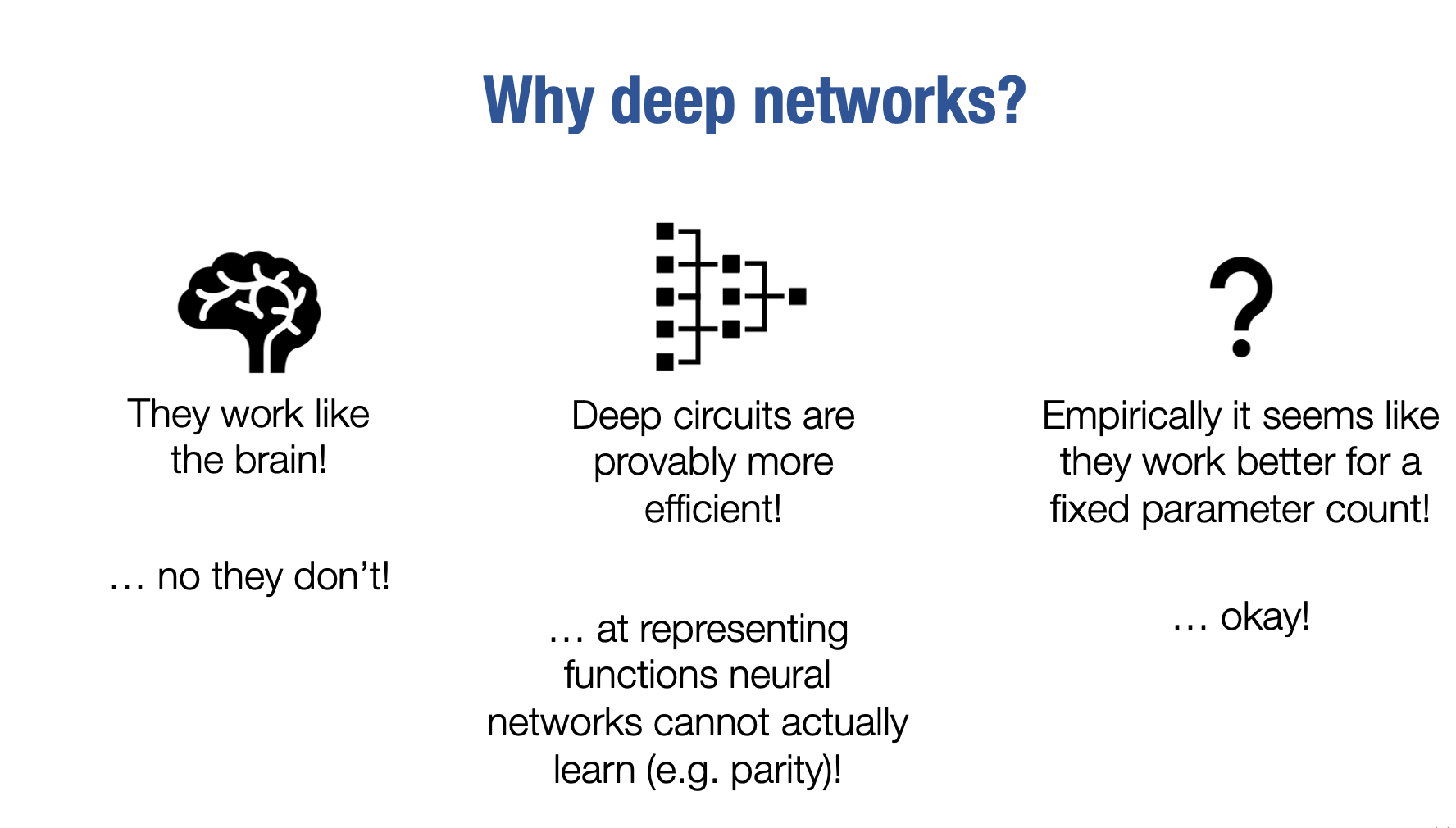
现在，当我们谈论深度网络时，您可能会立即想要问自己的一件事情是，为什么我们实际上要使用深度网络，对吧？我们为什么会使用深度网络呢？我们刚刚展示了单层或单隐藏层即两层网络已经是通用函数逼近器了。为什么我们要使用深度网络呢？实际上，人们给出了很多理由。我至少想提到其中一些关于为什么似乎我们如此关注深度学习以及为什么我们在展示出一个架构已经足够表示任何函数时，为什么我们使用深层网络的原因。我只展示了一维情况，但它在一般情况下也是正确的。人们给出了一些原因。其中第一个，又一次，与我之前提到的有关，神经网络至少在某种程度上受到大脑操作的启发。据我们所知，大脑在到达最终的决策中心之前会对其输入进行多阶段处理。然而，再次强调一下，这可能是一个很好的激励和启发性论点，但它并不能真正捕捉这些网络在实践中的工作方式。因此，我认为这是一个不好的论点，仅仅说，哦，大脑有层次结构，因此我们也需要层次结构。