Lec4.2 Automatic differentiation(1)

[TOC]

Reverse mode automatic differentiation

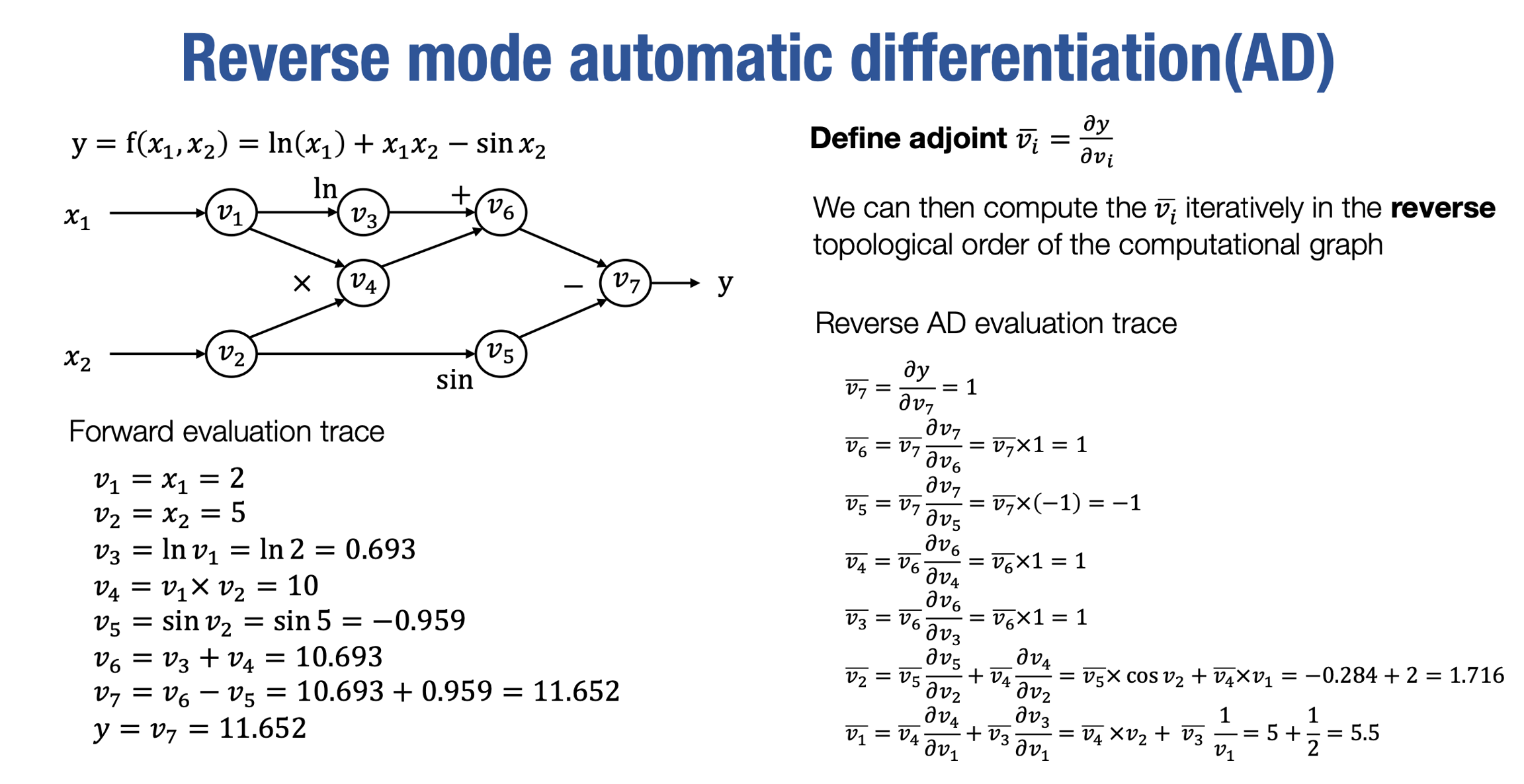
让我们开始推导反向模式自动微分。如果你手边有一支笔和纸，或者可以在你那边找到幻灯片，我强烈建议你跟随这些推导的幻灯片。我们将逐步推导每一步，并试着问自己在每一步推导中你是否真的确认它是正确的。这将是今天讲座的主要内容。

为了计算一个标量输出值相对于许多输入的梯度，我们将定义一个称为伴随（adjoint）的术语。伴随被定义为从输出标量到每个中间值节点的偏导数

\bar v_i=\frac{\partial y}{\partial v_{i}}

就像前向模式自动微分一样，我们将能够以更递归的方式推导它。与前向模式不同，这次我们希望从计算图的末尾开始推导，因为伴随的定义方式不同。

$\bar v_7$ 到 $\bar v_3$ 的推导还比较常规， $\bar v_2$ 值变得稍微有些有趣,在这里， $v_2$ 被 $v_4$ 和 $v_5$ 同时使用。所以我们希望能够考虑这两条路径：

\bar v_2= \bar v_4\frac{\partial v_4}{\partial v_{2}}+\bar v_5\frac{\partial v_5}{\partial v_{2}}

我们将在下一张幻灯片中对为什么会出现这种情况进行更详细的推导。同样，对于 $v_1$ ，它也同时使用了两条路径。你会发现有从两条路径传递回来的adjoint值和偏导数。

总结一下，通过定义adjoint值，我们可以从最末端递归地推导出每个计算图节点的adjoint值。我们从 $v_7$ 开始，因为该节点的adjoint值是微不足道的，即等于1。然后，对于每个节点，我们可以通过其下一个节点的adjoint值以及该输出节点对输入的偏导数来推导出adjoint值。

当我们得到v_1的adjoint值时，根据定义， $v_1$ 的adjoint值就是 $\frac{\partial y}{\partial x_1}$ 。而v_2的adjoint值是 $\frac{\partial y}{\partial x_{2}}$ 。将它们放在一起，实际上就得到了函数相对于所有输入x参数的梯度。

因此，反向模式自动微分真正使我们能够在单次反向传播中计算出标量函数相对于所有输入值的梯度。

Derivation for the multiple pathway case

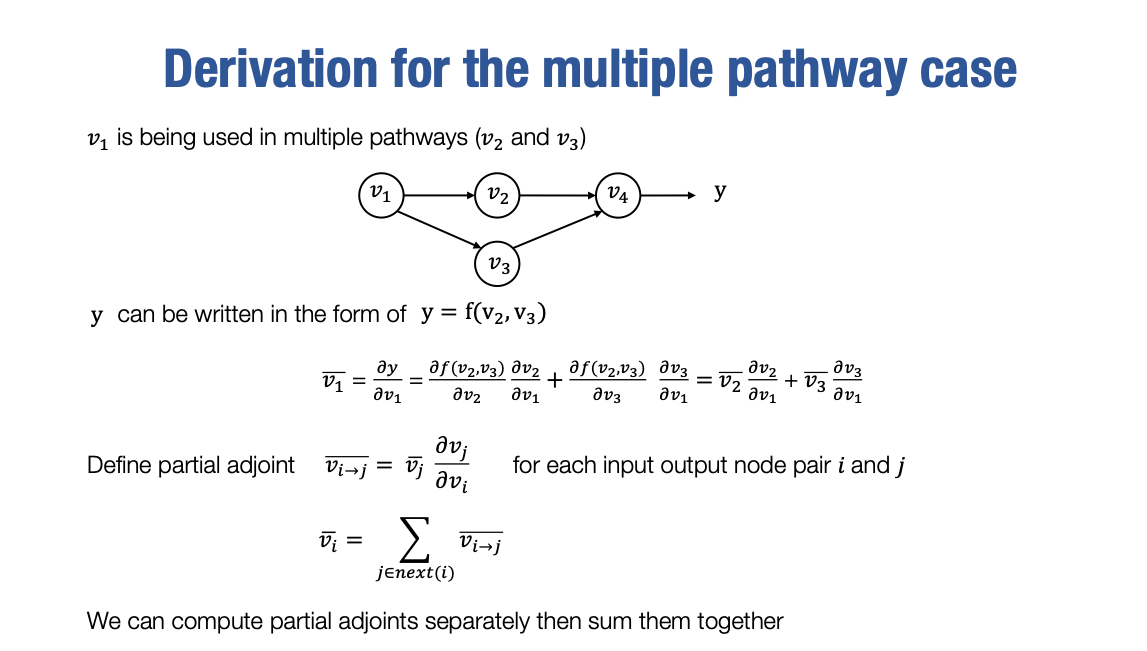
现在让我们更仔细地看一下多路径情况。我们刚才只是简单地介绍了多路径情况下的处理方式，以及为什么要将这些路径加在一起。

如果其他人告诉你说，我学会了自动微分，你肯定会问一个问题，即在单个输入值被多个输出值使用的情况下，你如何准确地推导出这种情况，并如何传递adjoint值。

让我们以一个例子来说明，其中 $v_1$ 被 $v_2$ 和 $v_3$ 同时使用:

\bar v_{1}=\frac{\partial y}{\partial v_{1}}=\frac{\partial f(v_2,v_3)}{\partial v_2} \cdot \frac{\partial v_2}{\partial v_{1}}+\frac{\partial f(v_2,v_3)}{\partial v_3} \cdot \frac{\partial v_3}{\partial v_{1}}=\bar v_{2}\frac{\partial v_2}{\partial v_{1}} +\bar v_{3}\frac{\partial v_3}{\partial v_{1}}

这就是正式的推导过程，它有点像你在微积分中学到的偏导数计算规则。因此，最终的 $v_1$ 的adjoint值将成为所有这些输出的adjoint值乘以相应输出对于输入节点 $v_1$ 的偏导数的和。

因此，实际上定义了一个称为"partial adjoint"的符号，表示特定adjoint的偏导数。例如，假设 $\overline{v_{i\rightarrow j}}$ 表示输出节点j的adjoint值和相应输出对于输入节点i的偏导数。

\overline{v_{i\rightarrow j}}=\overline{v_j}\frac{\partial v_j}{\partial v_{i}}

因此，通过将 $\overline{v_{1\rightarrow 2}}$ 和 $\overline{v_{1\rightarrow 3}}$ 相加，我们可以计算 $\bar v_1$ 。这符号表示对于我们正式编写自动微分算法和实现时非常有帮助。好的，到目前为止，我们已经手动推导了自动微分。可以看出，通过计算图和adjoint的定义，我们能够通过反向遍历计算图以递归的方式推导出中间梯度。

现在让我们开始思考如何使用Python代码或其他你喜欢的语言来实现该算法。

Reserve AD algorithm

算法的实现看起来像这样,但这是其中一种方式。

现在让我们仔细地走一遍这个具体的实现，因为这也是你们作业的第一部分，事实上，这将成为我们在本课程中进行的一切的基础。

首先，我将创建一个字典，将每个计算图节点映射到一个 partial adjoint的列表，这样我们可以在计算过程中部分地累积 partial adjoint。

根据我们之前的推导，我们知道输出节点的 partial adjoint为 1
然后我们可以反向遍历计算图，对于每个节点 i，首先要做的事情是，我们知道 node_to_grad 中包含了一个 partial adjoint 的列表。因此，我们将把它们求和以获得 $\bar v_i$ 。
一旦获得 $\bar v_i$ ,接下来要做的是计算每个输入的 partial adjoint。对于每个节点 k，从这个特定计算图节点的输入列表中，我们将通过计算公式
$\overline{v_{k \rightarrow i}}=\bar v_{i}\frac{\partial v_i }{\partial v_{k}}$

得到 $\overline{v_{k \rightarrow i}}$ ,然后我们将这个 partial adjoint 追加到 node_to_grad[k] 的值中，然后我们将在这里重复这个循环。

请记住，我们是按照反向拓扑顺序进行迭代的,这意味着当我们到达节点 i 时，我们已经访问了将 i 作为输入的所有节点。

这意味着 partial adjoint 列表,已经被填充了包含所有 partial adjoint 值的列表。这使得我们可以在这里将它们全部相加，

最后，在完成所有操作之后，我们将能够得到输入的 adjoint 值，然后将其返回给外部

这就是反向模式自动微分的实现。接下来，我将告诉你一个这个实现的变种,在我继续之前，我希望大家稍微停下来思考一下,你可能想要如何实现这个算法，特别是你会使用什么样的数据结构来表示 $\bar v_i$ 和 $\overline{v_{i \rightarrow j}}$ 。在这种情况下，一个自然的答案，可能是使用多维数组来存储这里的特定计算结果，这是一个非常合理的答案。

然而，在实践中，我们实际上并不这样做。

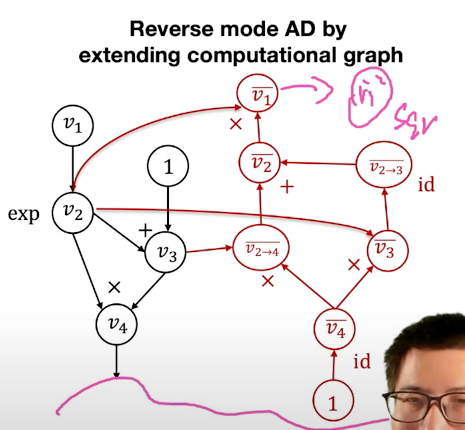
Reverse mode AD by extending computational graph

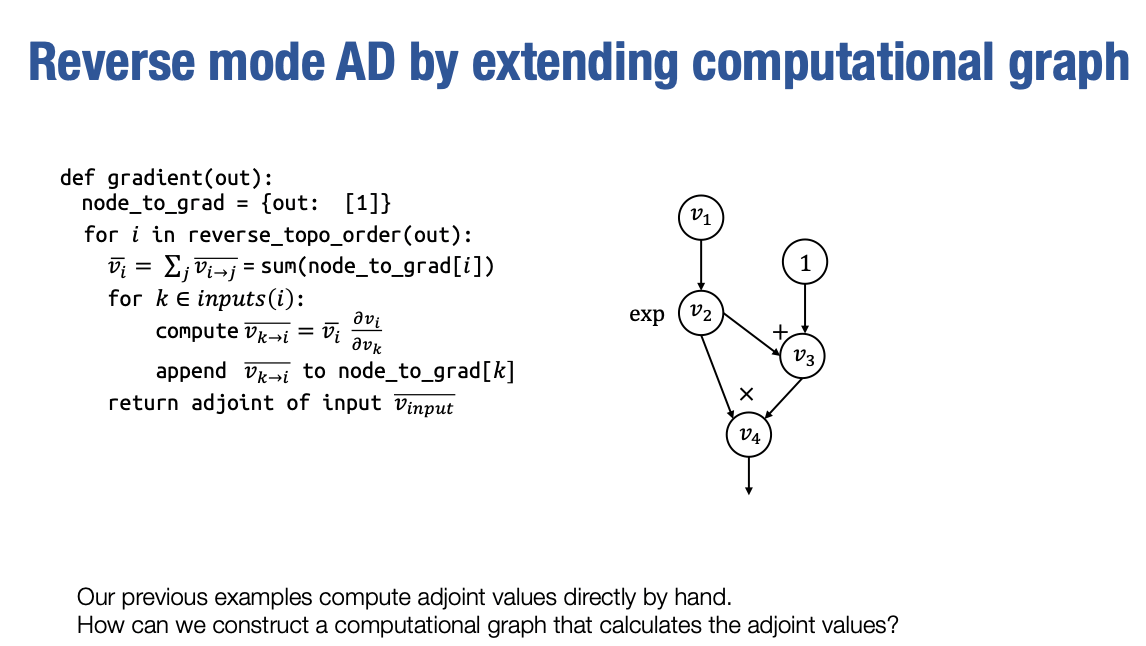
相反，我们将运行同样的算法，但是我们将构造一个计算图，而不是计算每个 $\bar v_i$ 和 $\overline{v_{i \rightarrow j}}$ 的实际具体值。

如果你不明白我的意思，等我们通过这个例子走一遍，你就会明白的。这里是我们将自动微分所涉及的计算图,我将在左边运行代码。这个计算图表示

v_2=e^{v_1}\\ v_3=e^{v_1}+1\\ v_4=(e^{v_1}+1)\cdot e^{v_1}

为了计算反向模式自动微分，我们将运行这个算法。

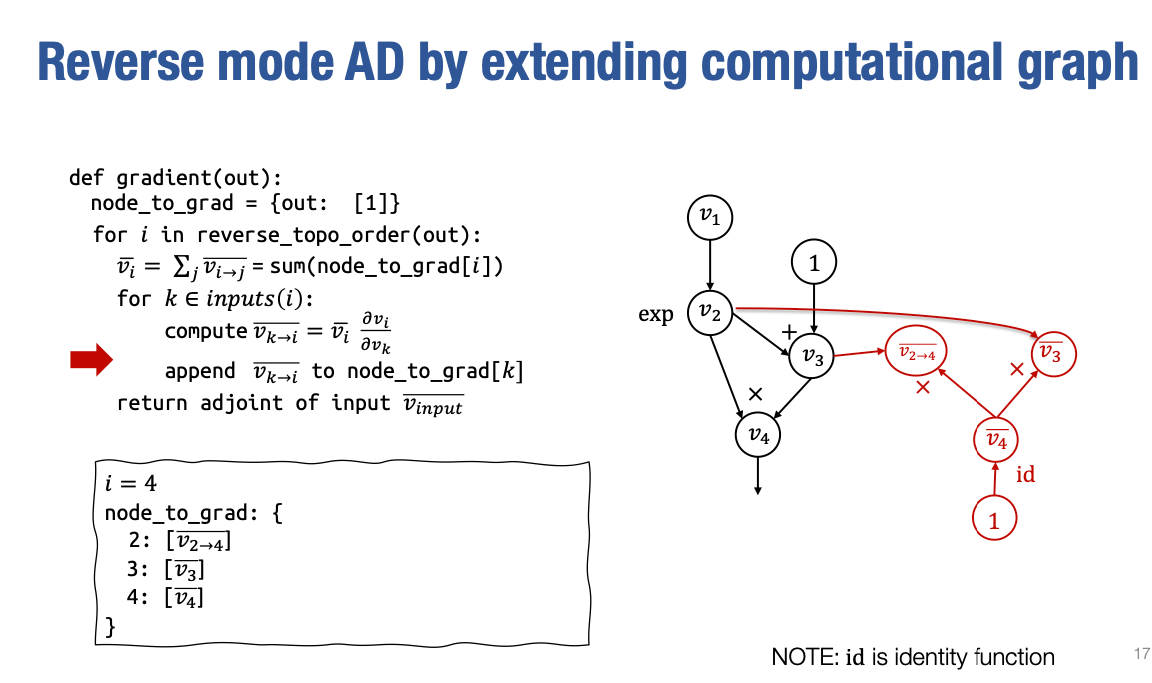
第一步，我们将计算当 i=4 时的 partial adjoint。所以我要计算 $v_4$ 的 adjoint 值。在这种情况下，我们知道 $v_4$ 的 adjoint 值为 1。所以我不会直接创建一个数组，表示 $\bar v_4$ 的值等于 1，而是在这里创建一个计算图节点。在这种情况下，id 是一个恒等函数，表示将输入直接输出。
第二步，遍历所有 $v_4$ 的输入，在这种情况下， $v_4$ 的输入是 $v_2$ 和 $v_3$ 。我需要计算 $v_2$ 和 $v_3$ 到 $v_4$ 的partial adjoint 的值:
$\overline{v_{2 \rightarrow 4}}=\bar v_{4}\frac{\partial v_4 }{\partial v_{2}}=\bar v_{4}\frac{\partial v_2\cdot v_3 }{\partial v_{2}}=\bar v_{4}v_3$
类似的
$\overline{v_{3 \rightarrow 4}}=\bar v_{4}v_2$
不过因为 $v_3$ 只有一个输出，所以 $\overline{v_{3 \rightarrow 4}}=\bar v_3$

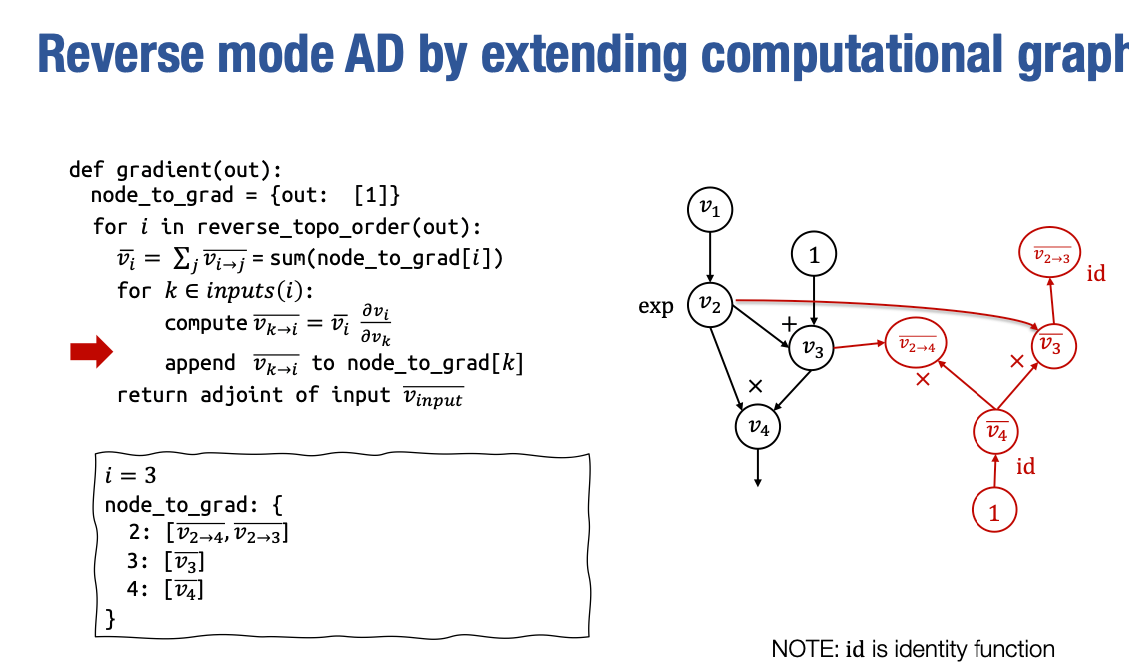
现在我们来看 i=3 的情况,在这种情况下， $v_3$ 只有一个输入节点，即 v_2，即加法函数。因此

\overline{v_{2 \rightarrow 3}}=\bar v_{3}

这就是为什么我们在这里放置一个恒等函数的原因。

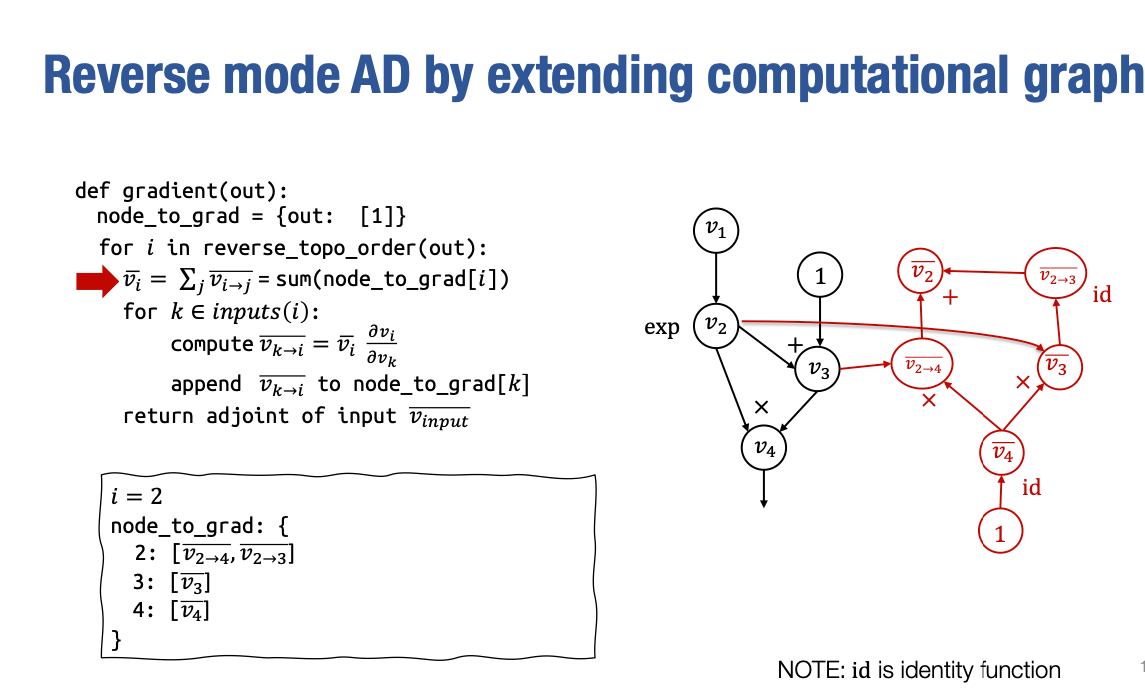
接下来是稍微有些有趣的部分。这是多路径情况， $v_2$ 被 $v_4$ 和 $v_3$ 使用，因此当我们到达这个特定迭代时，我们需要对这个列表求和。而这个列表在我们迭代 $v_4$ 和 $v_3$ 时已经被填充，其中包含 $\overline{v_{2\to3}}$ 和 $\overline{v_{2\to4}}$ 。在运行完这一步之后，我们将创建一个新的节点，表示 $\bar v_2$ 的 :

\bar v_2=\overline{v_{2\to3}}+\overline{v_{2\to4}}

最后，我们要计算 $\overline {v_{1\to2}}$ 。在这种情况下，由于 $v_1$ 只被一个地方使用，所以

\bar v_1=\overline {v_{1\to2}}=\bar{v_2}\frac{\partial v_2}{\partial v_1}=\bar{v_2}v_2

通过这种方式，我们可以避免额外的指数计算，而是通过创建节点来实现。

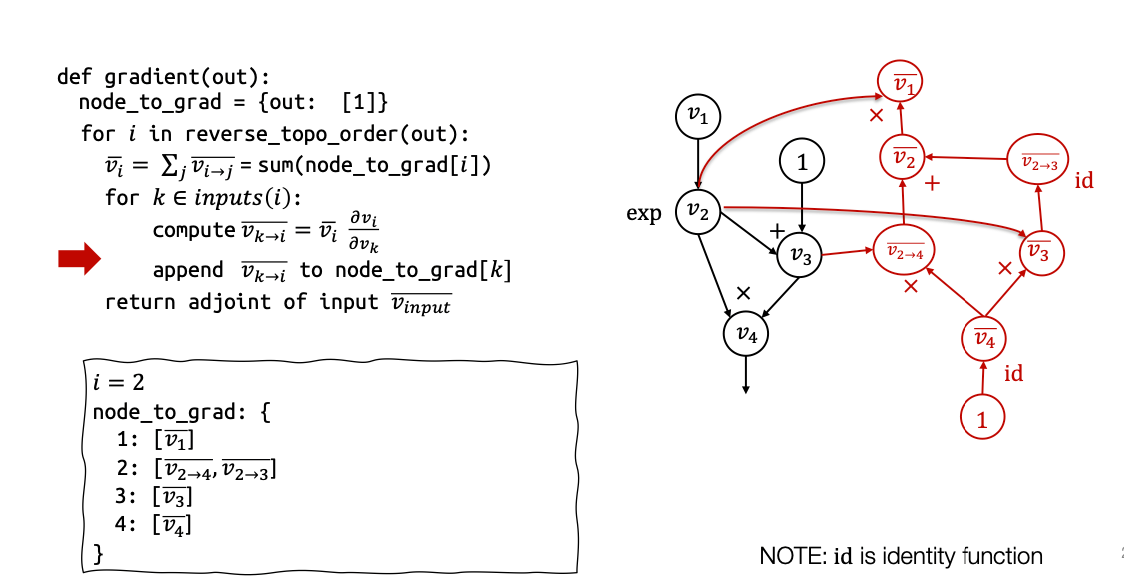
这就是我们运行这些反向模式自动微分计算的方法。在最后，你会发现与手动求导的情况不同，手动求导时我们写下每个计算的具体值，而这里我们创建了一个计算图。这是另一个扩展了原始计算图的计算图，它不仅包含了计算每个中间值的正向计算，还包含了计算梯度的反向计算。

这个计算图的一个令人惊奇之处是，与手动求导的情况不同，我们可以针对任意的 $v_1$ 值进行计算。我可以在这里设定 $v_1$ 为零，运行这个计算图，就能得到 $v_1$ 在 $v_1=0$ 时的 $\bar v_1$ 。如果我在这里设定 $v_1=2$ ，运行这个计算图，就能得到 $v_1$ 在 $v_1=2$ 时的 $\bar v_2$ 。

因此，这个特定的计算图可以用于不同种类的输入值，而无需从头开始运行自动微分的推导过程。这就是反向模式自动微分算法通过扩展计算图带来的一些微妙有趣的优势。而这也是现今大部分深度学习框架所使用的算法。

Reverse mode AD vs Backprop

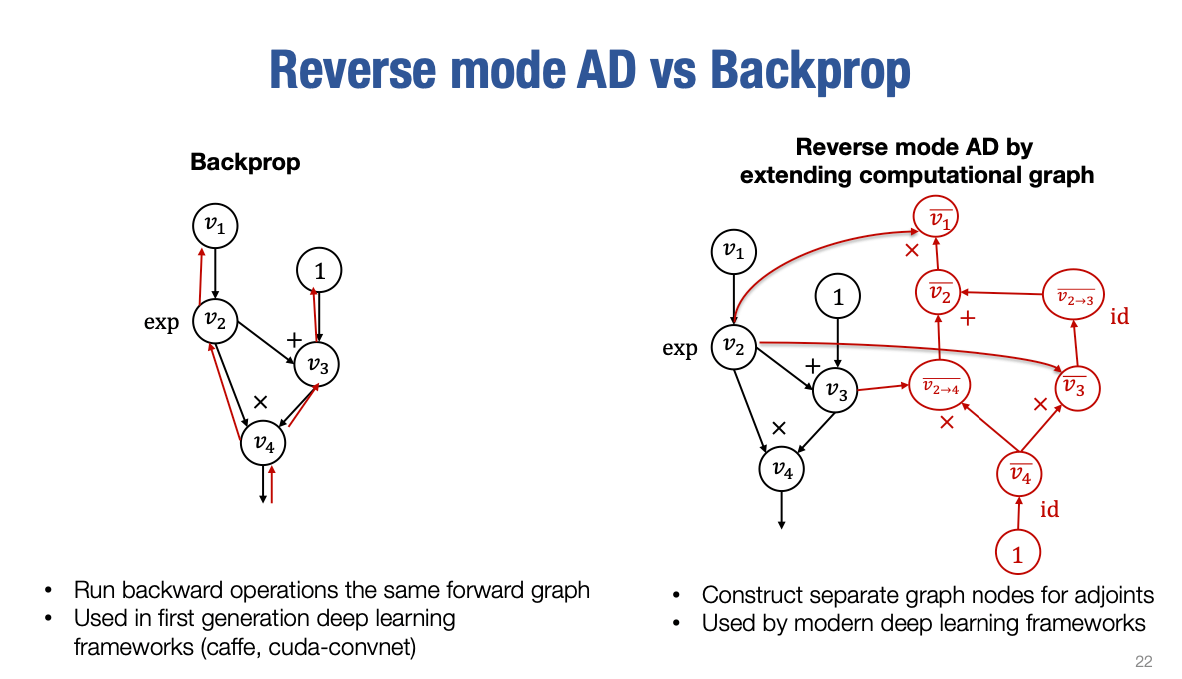
在上一堂课中，我们也谈到了反向传播。

所以你可能会有一个问题：**反向自动微分（Reverse Mode AD）**和我们在过去几堂课中讲的反向传播有什么区别？

大致上可以总结如下幻灯片。

当我们进行反向传播时，我们正在构建计算图，并且我们会向前运行计算以获取值。然后，当我们对梯度感兴趣时，我们直接在同一图上运行反向操作。因此，实际上，我们正在尝试向后运行，反向遍历原始计算图。在这个过程中，没有额外的计算图节点被创建。
事实上，这个反向传播方法是Geoff Hinton最初使用的方法，并且在第一代深度学习框架中使用，即Caffe和CUDA-ConvNet。当Alex Krizhevsky赢得了ImageNet挑战，深度学习真正起飞时，反向传播成为许多机器学习框架主要使用的算法，除了Theano。
Theano通过计算图引入了这种扩展计算图的反向自动微分方法。所以在第二代，当TensorFlow和PyTorch出现时，通过扩展计算图的方式的反向自动微分方法占据了主导地位。现在，大多数深度学习框架不使用直接在原始计算图中进行反向操作的反向传播算法。相反，它们总是尝试构建这个新的额外的梯度计算部分，对应于伴随计算。

我想在这里稍微停顿一下，让大家思考一下为什么。为什么现代深度学习框架通过扩展计算图的方式利用反向自动微分?

这背后有几个原因，既涉及到计算梯度的问题，也涉及到计算优化的简易性。

计算梯度的问题

首先，我们知道在某些情况下，当我们处理机器学习时，可能希望对梯度进行操作的一些损失函数。

例如，一个典型的损失函数可能是我想要最小化 ${\bar v_1}^2$ 。在这种情况下，我们想要定义一个损失函数，并对该输入变量求梯度，然后我希望能够对该梯度值的函数再次求梯度。在反向传播中，这很难做到，因为反向传播只定义并告诉你如何对输入进行梯度计算。所以它只会告诉你如何进行一次梯度计算，但是梯度的梯度怎么办呢？

可以通过扩展计算图的方式的反向自动微分，所以在这种情况下，我们可以添加一个名为"square"的节点，它实际上对 $v_1$ 的平方进行了计算

然后我们可以对这个计算图应用相同的自动微分算法，这将给出相对于 $v_1$ 的梯度函数的梯度值。因此，在某种意义上，通过构建这个扩展计算图的反向自动微分方法，你可以获得梯度的梯度。

这真的很酷，这是反向自动微分算法和计算图的一个非常酷的部分，你在作业中也会使用到。而令人兴奋的是，一旦你实现了这个自动微分算法，你可以得到梯度的梯度。

计算优化的简易性

通常使用扩展计算图的方式的反向自动微分的第二个原因是，梯度图的输出仍然是一个计算图。因此，为了评估这个计算图，我只需要关心向前运行这个图。这样，就有更多的机会来优化这些计算，例如，我可以将这两个节点合并在一起，因为它们是恒等函数，这将使得梯度计算不对称，不再有从前向计算到梯度计算的一一对应关系，但梯度计算可能会更有效率。因此，这也为底层的机器学习框架提供了更多优化梯度计算的机会。

好的，到目前为止，这是本次讲座的重点。

与gpt的对话

我可以理解计算梯度的时候需要多次反向传播，但是以计算 $\overline {(\bar v_1)^2}$ 为例，反向自动微分也需要先计算出 $\bar v_1$ 再反向求得梯度的梯度啊?
您是正确的，在计算高阶导数时，无论是传统的反向传播算法还是逆向模式自动微分方法，都需要进行额外的计算。对于计算 $v_1$ 的梯度的平方的平方，我们需要先计算一阶导数（梯度） $g = \frac{\partial f}{\partial v_1}$ ，然后再计算二阶导数（梯度的梯度） $h = \frac{\partial g}{\partial v_1}$ 。
在传统的反向传播算法中，我们需要进行两次反向传播。第一次反向传播计算梯度 $g$ ，第二次反向传播计算梯度的梯度 $h$ 。
而在逆向模式自动微分方法中，我们同样需要记录计算图上的每个节点的反向计算。在计算一阶导数 $g$ 时，我们记录了它的反向计算，包括求导的过程。当需要计算二阶导数时，我们可以直接通过反向计算来计算梯度的梯度$h$，而无需进行额外的计算。
因此，逆向模式自动微分方法相比传统的反向传播算法，在计算高阶导数时也具有一定的优势。虽然仍需要进行额外的计算，但它可以通过直接利用之前记录的反向计算来高效地计算梯度的梯度，而无需多次反向传播。
逆向模式自动微分方法会记录计算图上的每个节点的反向计算，但是传统的反向传播算法也会记录G_{i}啊?
您是对的，传统的反向传播算法也会记录每个节点的梯度G_i。在传统的反向传播算法中，计算图上的每个节点都会保存其对应的梯度，这些梯度将用于计算后续节点的梯度。这样，我们可以在反向传播过程中有效地传递梯度信息，并在需要计算高阶导数时进行相关计算。
逆向模式自动微分方法和传统的反向传播算法都会记录梯度信息，但它们在梯度计算的方式上略有不同。在传统的反向传播算法中，我们通过链式法则从输出层到输入层逐层传播梯度信息。而在逆向模式自动微分方法中，我们构建了一个扩展的计算图，并通过反向计算来获取梯度信息。
无论是哪种方法，计算高阶导数都需要进行额外的计算和存储开销。对于更复杂的计算图和更高阶的导数，这些开销可能会显著增加。因此，选择适当的方法和优化策略来计算高阶导数是非常重要的。

Reverse mode AD on Tensors

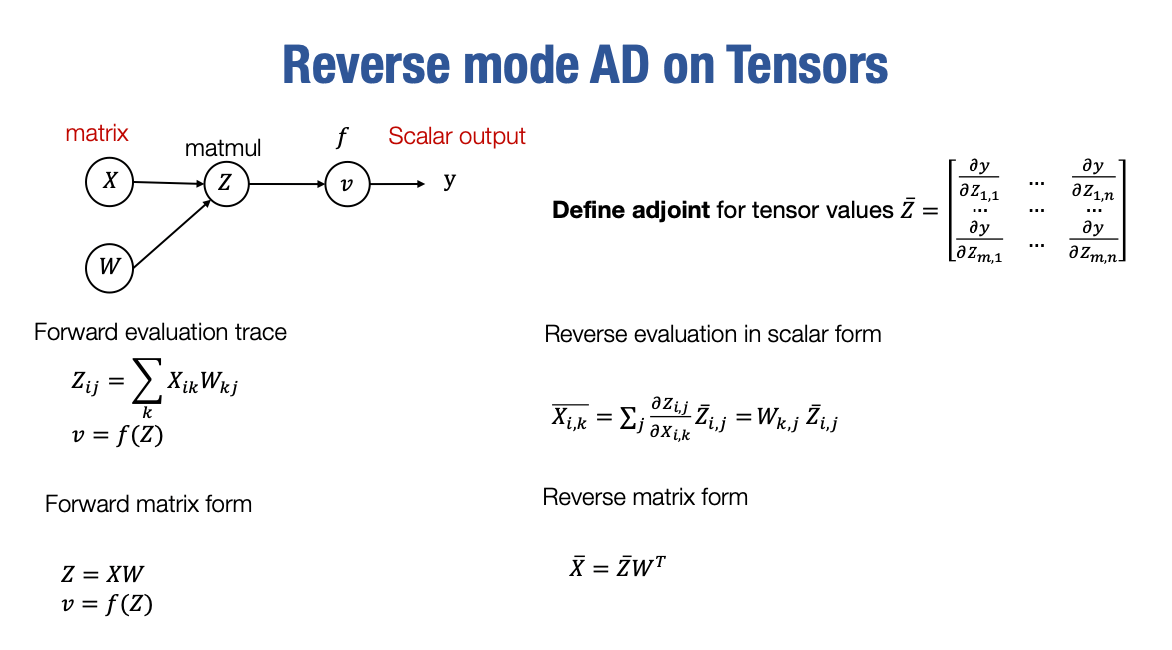
到目前为止，我们已经讨论了使用标量值进行自动微分的情况。实际上，当处理神经网络时，所有的中间值都是多维张量。而实际上，将我们的逆向模式自动微分方法推广到多维数组和张量上并不困难。

我们的做法是推广伴随的定义。对于一个矩阵 $Z$ ，也就是一个二维矩阵，或者一个张量，我们将定义该矩阵或张量的伴随为另一个矩阵，其中每个元素对应于该元素相对于伴随值的导数，因为相对于单个标量的导数是被很好地定义的。因此，我们可以利用这一点来定义张量的伴随值。

然后，我们可以使用标量自动微分规则推导出矩阵计算和张量计算的自动微分规则。

对于前向计算，我们知道 $Z_{ij} = \sum_k X_{ik} \cdot W_{kj}$ ，然后我们可以推导出特定元素 $X_{ik}$ 的伴随值和偏导数。我们知道特定的 $X_{ik}$ 被很多 $Z$ 值使用，对吗？所以我们希望能够将这些伴随值和偏导数进行求和。最后，我们知道 $\sum_j W_{kj} \cdot \overline{Z}_{ij}$ 。

在将其用标量形式推导出来后，可以将其写回矩阵形式。你会发现这个关系成立，其中 $X$ 的伴随值等于 $Z$ 的伴随值乘以$$W$$$的转置。这就是我们在神经网络计算中使用的常见规则，用于推导线性层的梯度。

因此，现在逆向模式自动微分可以推广到张量上。结果你会发现，对于张量和多维数组，实现方式基本保持不变。我们已经讨论了反向传播和逆向模式自动微分的优缺点，以及处理梯度的梯度的方法。

参看

[自动微分反向模式]{https://www.zhihu.com/question/320987507}

Reverse mode AD on data structure

所以最后，这是一个额外的幻灯片，我们已经讨论了逆向模式自动微分在张量上的应用。然而，当我们编写程序时，并不是所有的中间值都是张量。有时候我们可能想要将张量放在数据结构或其他形式中。例如，我们可以有一个字典，其中字典的每个值对应于我们想要相对于其进行微分的张量。实际上，我们可以将伴随的定义推广到这些数据类型和数据结构上。当然，我们可以推广定义。例如，在这种情况下，对于字典，我们可以通过确保字典键本身始终不是张量来推广定义。因此，它始终是一个我们可以相对于其进行微分的值，但其值可以是张量。我们可以将伴随定义为另一个字典，其中包含相同的键集，但值对应于相应的伴随值。因此，对于每个前向计算，比如字典查找，我们将能够定义一个反向计算梯度计算，其有效地构造另一个包含伴随值的字典。这里的关键是，对于不同的数据类型，只要我们可以为伴随值和伴随传播规则定义一个定义，我们就能够定义伴随计算。相同的逆向模式自动微分算法应该适用于这些情况。这是一种更一般的情况，称为可微编程，我们不会在本讲座和课程中涵盖这个概念。如果您对这个概念感兴趣，欢迎您搜索与可微编程相关的文献，您可以找到一些相关的资料。我们可能希望在作业中支持某些类型的数据结构。具体来说，我们可能希望为元组值添加支持，这意味着我们希望支持包含多个张量元组的值，并且我们希望能够为该特定元组值定义伴随值。因此，这将成为我们作业实现的一部分。感谢大家参加今天的讲座。在今天的讲座中，我们学习了为什么要进行微分以及一套工具，使我们能够同时检查自动微分实现的梯度以及实现逆向模式自动微分，以便我们可以在一次反向传递中获取所有输入的梯度值。最后，我们还讨论了如何通过扩展计算图来构建逆向模式自动微分算法，以便我们可以使用相同的工具来获得梯度的梯度，并在低级优化方面

PreviousLec4.1 How does differentiation fit in machine learning NextLec5